Индексы в определении свертки последовательностей [или функций].
Попытка объяснения необычных индексов в определении операции свёртки.
Содержание:
- Введение
- Немного определений
- Умножение чисел
- Корреляция
- Линейные системы
- Заключение, выводы
- Ссылки
Введение
Что общего между поиском котов на фотографии, сжатием музыки, прогнозированнием курсов валют, угадыванием мелодии по нотам, умножением чисел на бумаге (или на счётах), и добавлением, скажем, эффекта звучания в большом железобетонном зале к речи, записанной на улице?
А общность их заключена хотя-бы в том, что с точки зрения программиста, все эти задачи (причем, список подобных — на первый взгляд разрозненных — примеров на самом деле длиннее) могут быть более или менее успешно решены практически одним и тем же небольшим куском кода, реализующим свёртку [1] функций или последовательностей. (С точки зрения же заказчиков и управляющих/начальства этого программиста, такие задачи должны, конечно, считаться абсолютно не связанными друг с другом и, соответственно, требующими отдельного независимого финансирования. :) )
Взглянув на первое попавшееся определение свертки, некоторым нелегко сразу понять, почему в формуле записаны минусы в индексах, и почему при наглядной интерпретации в виде наложения графиков требуется сначала отразить один из них.
В настоящем сообщении я хотел бы показать естественность свертки используя ряд простых примеров, среди которых будут перемножение чисел, теорема о свертке и рассуждения о сдвиговой инвариантности линейных преобразований.
Немного определений
Циклической (или круговой) свёрткой двух последовательностей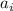 
и 
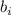длины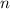 
называют
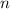-элементную последовательность 
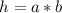с элементами
Выражение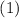 
может быть записано и более симметричным образом (обратите внимание, что такая
запись уже позволяет избавиться от минусов, правда ценой переноса слагаемого в индекс/предел
суммы):
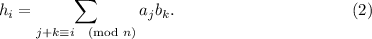
Теорема о свертке:
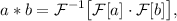
где
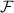– преобразование Фурье; причем перемножение Фурье-образов производится поэлементно.
В словесной формулировке можно сказать, что спектр свертки равен произведению спектров исходных сигналов.
Набросок доказательства (из [2]):
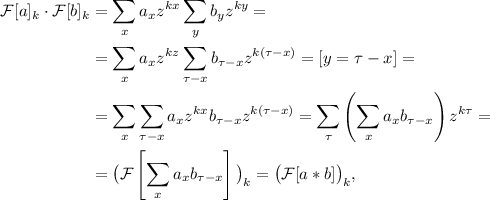
где
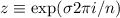и используется определение преобразования Фурье для
последовательности: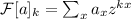 
(здесь игнорируется небольшое отличие
между прямым и обратным преобразованиями Фурье, заключающееся в знаке аргумента экспоненты и
в множителе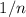 
[перед обратным преобразованием]). 
Аналогичный результат известен и для преобразования Лапласа:
.
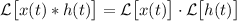Уместно заметить, что теорема о свертке имеет важное прикладное значение, т.к. дает метод эффективного вычисления свертки с помощью быстрого преобразования Фурье [3]. В нашем же случае важно видеть как в приведенном простом доказательстве появляются минусы в индексах и, что гораздо более интересно, как они используются далее для преобразования границ суммирования.
Линейной (или ацикличной) свёрткой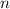 
-элементных последовательностей 
и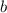 
называется
последовательность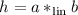 
длины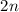 
, с элементами:
Линейная свертка может быть найдена с помощью циклической свертки если исходные последовательности
длины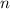 
дополнить нулями до длины 
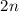, а затем свернуть.
Линейная свертка фактически может рассматриваться как произведение чисел — суть строк цифр [в некоторой позиционной системе счисления], — или как произведение полиномов.
Определение свертки обобщается и на непрерывный случай. А именно, есл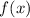и 
и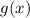 
– непрерывные
функции, то их свертка равна
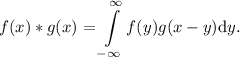
N.B., этот интеграл тоже является функцией от 
. (Вопросы, связанные с квадратичной интегрируемостью
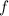функций 
и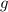 
здесь не рассматриваются.)
Умножение чисел
Перемножим два целых положительных числа 
и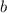 
, имеющих десятичные разложения
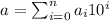и
,
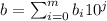соответственно, где 
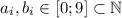. Результат будет равен
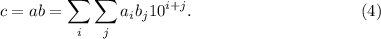
Но если мы построим подобное разложение и для 
, т.е. запишем его как
где
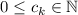(N.B., здесь, в отличии от разложений для 
и
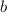мы не используем неравенство 
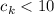, позволяя такой записи числа оставаться
«ненормализованной», т.е. возможно требующей серии дальнейших переносов в старший разряд), то
приравнивая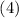 
и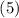 
мы получим выражения для «цифр» числа 
: 
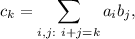
где применено равенство
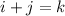из-за того, что в слагаемом 
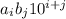разложения 
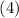множитель 
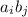находится при степени десяти 
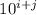, а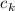 
в
разложении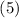 
находится при 
.
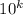Из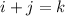 
можно выразить 
как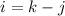 
. Подстановка в выражения для 
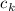дает:
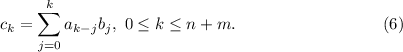
Сравнение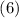 
с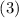 
показывает, что мы здесь имеем дело именно с линейной сверткой
последовательностей цифр исходных чисел 
и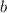 
. (Достаточное количество переносов в старший
разряд, выполненных в произвольном порядке, позволит преобразовать каждое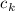 
в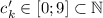 
, т.е. в настоящую цифру числа 
.)
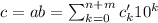Корреляция
Для непрерывных функци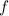й 
и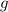 
, их корреляция (или кросс-корреляция) [4] определяется как
(
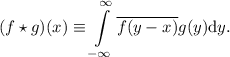
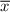обозначает комплексное сопряжение некоторого числа 
.)
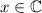Это определение можно записать в эквивалентной форме, без минуса:
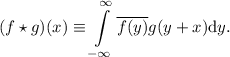
Есл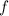и 
и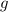 
периодичны с периодом 
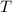, то можно интегрирование производить по
интервалу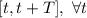 
.
Связь корреляции со сверткой:
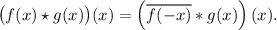
Интересное свойство:
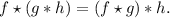
Аналог теоремы о свертке; привожу без доказательства (которое, однако, легко построить
по аналогии с вышеприведенным случаем для обычной теоремы о свертке):
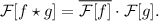
Также как и в случае со сверткой, мы можем ограничиться рассмотрением значений функций в отдельных точках, что после замены интегралов знаками суммы приводит к аналогичным формулам для числовых последовательностей.
Линейные системы
Широкое практическое применение свертки (в частности физиками и инженерами) обусловленно возможностью её использования для описания отклика линейных систем, в том числе многих реальных физических систем, обладающих свойствами линейности и сдвиговой инвариантности (симметричности) по времени (или заменяющей(-им) его переменной(-ым)).
(Ниже, в основном, приведена свободная адаптация материала из [5] с некоторым упрощением нотации, и не факт, что без ущерба строгости изложения. Кроме того, я ограничусь рассмотрением только непрерывного случая, подразумевая, что дискретная версия вытекает из него как частный случай.)
Допустим, некоторая система моделируется функцией 
, преобразующей входной сигнал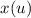 
в отклик
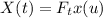. Отображение 
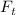(фактически, оператор) линейно:
.
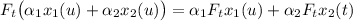Последнее выражение, очевидно, легко обобщается и на произвольное количество слагаемых-сигналов
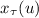и на непрерывный случай с заменой суммирования
интегрированием:
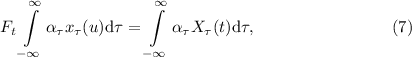
где
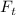преобразует
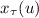в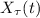 
.
Кроме этого, отображение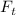 
инвариантно относительно сдвигов [по «времени»]:
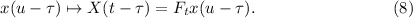
Т.е. в данном случае моделируется важное свойство реальных систем, а именно независимость результатов эксперимента от времени его начала: если мы опоздали с началом эксперимента на некоторое время
, то и результаты мы получим
с опозданием 
.
Так как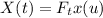 
, то (просто за счет подстановки 
)
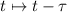Если в качестве сигнала взять [одномерную] дельта-функцию Дирака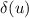 
[6,7], равную нулю всюду за исключением единственной
точки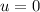 
(в которой она равна бесконечности) и моделирующую идеальный импульс [бесконечно
малой продолжительности], то с помощью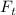 
мы получим импульсный отклик 
.
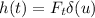Это выражение с использованием уравнени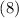й 
и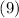 
приводит к
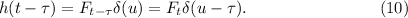
Интересно, что несмотря на de-facto определение
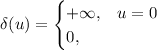
интеграл по всему пространству равен 1:
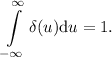
Причем из этого уравнения следует фильтрующее свойство
-функции (для некоторой функции 
):
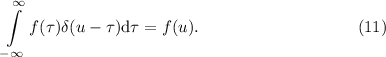
Доказательство фильтрующего свойства.
Т.к.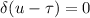 
при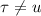 
, то интеграл 
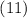не зависит от значений 
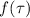при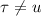 
, а зависит только от значения в единственной точке 
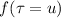. Поэтому функцию
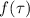можно просто заменить константой 
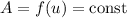, которую можно будет вынести
за знак интеграла:
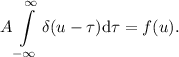
Но теперь оставшийся интеграл равен единице (несмотря на другие переменные, это всё-равно интеграл от дельта-функции по всему пространству) и
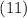превращается в тождество 
.
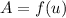Возможно расчитать отклик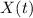 
системы на некоторый входной сигнал 
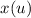не зная
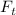в явном виде, а только располагая импульсным откликом 
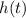. Именно (используется коммутативность
свертки):
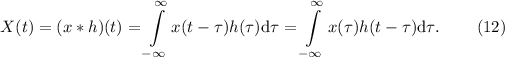
Демонстрация адекватности свертки для описания [сдвигово-инвариантных] линейный систем может быть
произведена с помощью доказательства справедливости уравнения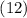 
.
Набросок доказательства.
Подстановка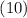 
в выражение 
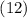для свертки даёт:
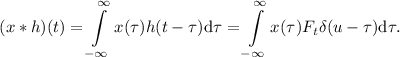
Используя выражаемую уравнением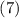 
линейность, т.е. вынося 
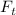за знак интеграла, получаем:
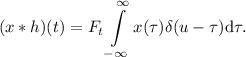
Применяя фильтрующее свойство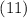 
дельта-функции, а также определение 
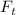как отображения
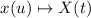, приходим к уравнению 
.
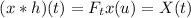Таким образом, справедливость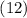 
доказана. 
Заключение, выводы
Как видно из вышеприведенных примеров, свертка является достаточно естественной концепцией, всем хорошо знакомой по умножению многозначных чисел (подходит для демонстрации линейной свертки). Теорема о свертке тоже выглядит достаточно просто (и подходит для демонстрации циклической свертки). Причем из обоих примеров сразу становится понятным происхождение «необычных» индексов в определении свертки последовательностей (и не менее «необычных» аргументов у функций в непрерывном случае).
Интересно, что корреляция, не требующая отражения графика одной из функций при наглядной интерпретации, и могущая быть записанной без вычитания в выражениях для индексов/аргументов, оказывается даже более отдаленной от прикладного, «бытового» применения математики; а аналог теоремы о свертке в случае с корреляцией требует использования лишней операции комплексного сопряжения.
Наконец, продемонстрирована самосогласованность операции свертки при описании достаточно большого класса реальных систем (со свойствами линейности и сдвиговой инвариантности).
Ссылки
- 1. http://en.wikipedia.org/wiki/convolution
- 2. Arndt J. Matters Computational
- 3. http://en.wikipedia.org/wiki/Fast_Fourier_Transform
- 4. http://en.wikipedia.org/wiki/cross-correlation
- 5. http://en.wikipedia.org/wiki/linear_time-invariant_system
- 6. http://en.wikipedia.org/wiki/Dirac_delta_function
- 7. http://ru.wikipedia.org/wiki/дельта-функция