Занимательное квайноводство. Часть I.
В этом сообщении (в первой части серии сообщений), после краткого введения в некоторые основы теории вычислимости, в основном описываются результаты простого эксперимента по автоматизированному конструированию квайна с использованием второй рекурсивной теоремы Клини.
В качестве целевого языка выбран язык поточного редактора [GNU] sed. Изложение, однако, не специфично для этого языка и может трактоваться в более широком контексте. Фактически, в предлагаемом цикле сообщений излагаются некоторые подходы к систематическому конструированию квайнов.
Содержание:
- Введение в квайнологию
- Вводные замечания
- Неподвижные точки вычислимых функций
- Главный эксперимент
- Промежуточные итоги
- Дополнительная теория
- Немного о пределах познаваемости
-
Другие подходы и «слегка открытые» вопросы
- «Креацианизм» vs. «абиогенез»
- Кимианские квайны и итеративное вычисление неподвижной точки
- Другие конструктивные теоремы о неподвижной точке
- Комбинатор неподвижной точки в лямбда-исчислении
- Логическое программирование в ограничениях
- Эволюционные алгоритмы
- Цепные квайны
- Генератор квайнов, не зависимый от языка
- Заключение
- Ссылки
Введение в квайнологию
Всем известно «стандартное» упражнение в программировании, заключающееся в написании программы, печатающей свой собственный текст. За такими самореплицирующимися программами достаточно давно закрепилось название «квайн» (также встречаются варианты написания/произношения «куайн», «квин», «куин») введенное в известной книге Хофштадтера [26] в честь философа Куайна (Уиллард Ван Орман Куайн = Willard Van Orman Quine) и его «парадокса Куайна» [15].
Сами квайны при этом появились раньше. Может быть их историю следовало бы вести с работ фон Неймана по самореплицирующимся [клеточным] автоматам [9, 48] или даже с работ Чёрча и Хаскеля…
Квайны являются немного парадоксальными программами, в соответствии с бытовой интуицией не могущими существовать, – ведь может показаться, что программа не может вывести текст, имеющий длину, равную длине самой программы (должно остаться место для кода, выполняющего печать). И тем не менее они существуют (и не требуют сжатия данных, которое, в соответствии с фундаментальной теоремой компрессии, не всегда возможно).
Более того, теория вычислимости говорит, что квайны можно написать на любом [достаточно выразительном] языке программирования. На деле, конечно, сложность написания и размер результирующего кода сильно варьируются от языка к языку.
В качестве примеров квайнов можно привести такие поделки (авторы мне не известны):
Квайн на lisp:
((lambda (x)
(list x (list (quote quote) x)))
(quote
(lambda (x)
(list x (list (quote quote) x)))))
Квайн на стековом rpn-языке форт (forth):
s" 2dup 115 emit 34 emit 32 emit type 34 emit type cr bye"
2dup 115 emit 34 emit 32 emit type 34 emit type cr bye
(Это одна длинная строка, могущая отображаться на нескольких экранных строках.)
Квайн на экспериментальном функциональном стековом rpn-языке joy [32]:
"dup.putchars.10 putch."
dup.putchars.10 putch.
Квайн для 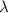 -исчисления(почти то же, что и выше на lisp):
-исчисления(почти то же, что и выше на lisp):
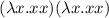
В стандартной библиотеке языка C есть функция форматированного вывода printf, которая может
быть использована [в качестве суррогата 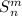 -функции] для внедрения текста программы в него
самого; что-то вроде
-функции] для внедрения текста программы в него
самого; что-то вроде printf(f, f), только с учетом технических сложностей с вложенными
кавычками для обрамления строк. По этому принципу построен такой известный однострочный
миниквайн на C (здесь не указан заголовочный файл stdio.h, в котором определена printf, но в
таком виде этот код всё-равно компилируется и работает):
char*f="char*f=%c%s%c;main(){printf(f,34,f,34,10);}%c";main(){printf(f,34,f,34,10);}
Многие квайны (в т.ч. большинство из приведенных выше) злоупотребляют экранированием строк, специальными кодами символов (зависящими от используемой в системе кодировки, e.g. ASCII) и библиотечными функциями подстановки (замены подстрок), «скрывающими» существенную часть происходящих процессов. «Идеологически» более чистым подходом представляется ограничение строковых манипуляций конкатенацией строк при одновременной минимизации экранирований. Неплохим образчиком подобной стратегии написания квайнов является квайн (на pascal’е) от Dan Hoey (взятый мною из [50]):
program s;const bbb='program s;const bbb';a='a';b='b';bb=');writeln(';
aa='''';ab='=''';ba=''';';
aaa='begin writeln(bbb,ab,bbb,ba,a,ab,a,ba,b,ab,b,ba,b,b,ab,bb,ba';
aba='a,a,ab,aa,aa,ba,a,b,ab,ab,aa,ba,b,a,ab,aa,ba,ba';
abb='a,a,a,ab,aaa,ba);writeln(a,b,a,ab,aba,ba);writeln(a,b,b,ab,abb,ba';
baa='b,a,a,ab,baa,ba);writeln(b,a,b,ab,bab,ba);writeln(aaa,bb';
bab='aba,bb);writeln(abb);writeln(bb,baa);writeln(bb,bab)end.';
begin writeln(bbb,ab,bbb,ba,a,ab,a,ba,b,ab,b,ba,b,b,ab,bb,ba);writeln(
a,a,ab,aa,aa,ba,a,b,ab,ab,aa,ba,b,a,ab,aa,ba,ba);writeln(
a,a,a,ab,aaa,ba);writeln(a,b,a,ab,aba,ba);writeln(a,b,b,ab,abb,ba
);writeln(b,a,a,ab,baa,ba);writeln(b,a,b,ab,bab,ba);writeln(aaa,bb
);writeln(aba,bb);writeln(abb);writeln(bb,baa);writeln(bb,bab)end.
(N.B., на самом деле этот квайн записывается в одну строку.)
Неплохое введение в написание квайнов можно найти, например, в [1, 30]; а неплохую коллекцию – в [30, 18].
Искусство versus ремесло
Основной причиной проведения небольшого эксперимента, ставшего основой настоящего сообщения,
явилось желание написать, или, точнее говоря, попробовать написать квайн на входном языке
поточного редактора sed. Применение поисковых систем для поиска уже имеющихся решений привело к
обнаружению квайна quine.sed [17] из «музея квайнов» [18] (автор: Tsuyusato Kitsune):
s/^/s11^113311;h;s221[1]221122g;s112[2]11222211g;G;s11^22([^3]*22)3322([^22n]*22).22(.*22)$1122122322211/;h;s\1[1]\/\g;s/2[2]/\\/g;G;s/^\([^3]*\)33\([^\n]*\).\(.*\)$/\1\3\2/(N.B., это одна строка текста.)
Вряд ли у меня вышло бы улучшить (например, сократить) этот квайн. Более того, самостоятельная попытка написать нечто подобное тоже не увенчалась успехом. Поэтому было принято решение действовать более систематичным образом и воспользоваться уже имеющимся в распоряжении математики арсеналом готовых теоретических средств.
Вторая рекурсивная теорема Клини имеет своим следствием утверждение о существовании квайна для любого языка программирования, а конструктивный характер её доказательства дает готовый рецепт для написания такого «саморепликатора» (ниже об этом будет написано подробнее).
Стандартные пособия по теории вычислимости нередко не ограничиваются лишь утверждениями о
существовании квайнов, и даже приводят конкретные примеры их конструирования, правда, выбирая
при этом, как правило, «удобные» языки программирования, например, прагматические реализации
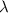 -исчисления, такие как lisp и его производные.
-исчисления, такие как lisp и его производные.
Попадались интересные исключения, e.g. [35, 36], но для слишком абстрактных машин. Поэтому я решил повторить классический эксперимент с конструированием квайна на основе доказательства рекурсивной теоремы Клини, но выполнить этот эксперимент на языке sed (кстати, всё-равно оказавшемся достаточно удобным для этой задачи, в основном из-за возможности объединения скриптов их конкатенацией).
Обновление (август, 2020): Уже после написания черновика этого сообщения, примеры применения второй рекурсивной теоремы Клини к практическим языкам программирования всё-таки отыскались на просторах интернета. В [53] можно найти генератор квайнов на JavaScript (ECMAScript), а в [54] – похожий генератор, но для C++. Причем в последнем примере, указанная утилита позиционируется как достаточно общий инструмент для добавления рефлексивных возможностей к языку, с ограниченной штатной рефлексией (i.e., сгенерированная программа может как просто печатать свой собственный текст, так и вычислять произвольные функции от него, скажем, находить свою длину).
Возможно читателю также будет интересна аналогичная утилита [55], преобразующая произвольную программу на C в квайн.
Результаты эксперимента говорят о возможности автоматической, или «нетворческой» генерации квайнов, в том числе и на sed.
Эффективность и выбор названия серии сообщений.
Быть может некоторым показалось бы несколько более благозвучным слово вроде «квайноделия», но «квайноводство» подходит куда лучше… От части потому, что, как и обещают стандартные вводные курсы по теории вычислимости, квайны, конструируемые прямым применением [второй рекурсивной] теоремы Клини, обычно получаются, мягко говоря, «неэффективными», как по времени, так и по пространству. Ещё одной метрикой эффективности может быть отношения объёмов данных и кода; специально я не исследовал этот вопрос, так что не могу сказать как с этим обстоят дела у автоматически сгенерированных квайнов, но неверняка неоптимально. :)
Постановка задачи
Пусть квайн хранится в исполняемом файле quine, полученным компиляцией его исходного текста из
файла quine.source. Для меня достаточно чисто формального выполнения следующего теста:
./quine any_argument > quine.output
diff quine.source quine.output
или аналогичного теста для интерпретируемого языка (здесь interpreter – исполняемый файл
интерпретатора или аналогичная внутренняя команда оболочки):
interpreter quine.source any_argument > quine.output
diff quine.source quine.output
Для sed это соответствует следующему тесту:
echo any_argument | sed -f quine.sed > quine.output
diff quine.sed quine.output
Проверку на тривиальность (в частности, на пустоту) можно выполнять и «вручную» (из-за плохой формализуемости и некоторой субъективности).
То есть, квайн конечного размера (скажем, помещающийся на жесткий диск) должен напечать свой собственный текст за конечное (и разумное время). Абсолютно не важно, будут ли исходный текст и скомпилированная программа весить несколько килобайт или несколько мегабайт. Гораздо важнее, чтобы квайн был истинным, т.е. был непустым, «содержательным», и не использовал «нечестные» рефлексивные возможности (вроде чтения своего исходного текста из файла).
Вводные замечания
В теории вычислимости особо важное место занимают несколько интересных теорем о вычислимых функциях. В этом сообщении я хотел бы кратко рассказать об этих теоремах и о некоторых их применениях.
Для некоторой программы с текстом 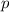 соответствующую ей (частичную) вычислимую функцию обычно
обозначают как
соответствующую ей (частичную) вычислимую функцию обычно
обозначают как 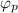 , однако, воизбежание нагромождения нижних индексов далее будет
использоваться несколько более удобное обозначение, широко применяющееся при изучении семантики
языков программирования, а именно
, однако, воизбежание нагромождения нижних индексов далее будет
использоваться несколько более удобное обозначение, широко применяющееся при изучении семантики
языков программирования, а именно 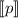 .
.
Обычно, в теории алгоритмов (теории вычислимости, теории рекурсии) говорят о [гёделевском] номере программы, а не о её тексте, но далее будет использоваться более наглядное и привычное, по крайней мере для программистов, слово текст, иногда даже исходный код, без прямого отсыла к понятию нумерации из теории вычислимости. Более того, вразрез с традиционным словоупотреблением, в настоящем сообщении нередко программа и её текст будут отождествляться, – здесь это просто одно и то же. (Краткости и простоты ради, это сообщение будет вообще несколько неформальным и не строгим.)
При одновременном рассмотрении нескольких языков программирования, как, например, при
работе с трансляторами, можно указывать язык программирования в нижнем индексе
семантических скобок, e.g., 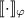 . (Кстати, в литературе
встречается и более необычная нотация, например, вообще не используюшая какие-либо индексы и
скобки, для экономии места.)
. (Кстати, в литературе
встречается и более необычная нотация, например, вообще не используюшая какие-либо индексы и
скобки, для экономии места.)
Символом  будет обозначено незавершающееся вычисление, т.е.
будет обозначено незавершающееся вычисление, т.е.  – это значение
бесконечного цикла. Равенство
– это значение
бесконечного цикла. Равенство 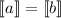 есть сокращение
для
есть сокращение
для 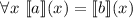 . (Подразумевается, что
для некоторых
. (Подразумевается, что
для некоторых  , может выполнятся
, может выполнятся 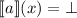 и
и 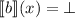 .)
.)
Теорема об универсальной функции
Сначала хотелось бы упомянуть теорему о существовании универсальной программы, а фактически о
возможности написания интерпретаторов для любых подходящих (Тьюринг-полных) языков
программирования, причем подразумевается, что интерпретатор пишется на его же входном языке.
Более формально, эта теорема утверждает, что существуют вычислимая функция — универсальная
функция —  , а также соответствующая ей программа-интерпретатор
, а также соответствующая ей программа-интерпретатор 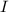 , такие, что для любой
программы
, такие, что для любой
программы 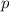 , интерпретатор может быть запущен с несколькими аргументами, первый из которых
равен
, интерпретатор может быть запущен с несколькими аргументами, первый из которых
равен 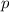 , а оставшиеся суть просто аргументы для этой программы. Так запущенный интерпретатор
должен возвратить тот же результат, что и сама программа
, а оставшиеся суть просто аргументы для этой программы. Так запущенный интерпретатор
должен возвратить тот же результат, что и сама программа 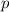 при тех же аргументах.
при тех же аргументах.
То есть, 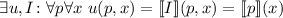 .
.
Набросок доказательства.
Доказательство может проводится просто предъявлением готового интерпретатора в виде машины
Тьюринга, т.е. путем построение т.н. универсальной машины Тьюринга, симулирующей работу любой
другой машины Тьюринга. Понятно, что можно использовать и любую другую модель вычислений, e.g.,
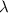 -исчисление. Но здесь, для краткости, аргументация будет менее конструктивной и более
абстрактной.
-исчисление. Но здесь, для краткости, аргументация будет менее конструктивной и более
абстрактной.
Естественно считать программами куски текста (i.e., строки) на некотором языке программирования.
Пусть на строках определён обычный порядок 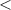 , а именно, для строк
, а именно, для строк  и
и  выполняется
выполняется 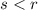 если
если 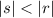 (i.e., сравниваются длины) или, в случае
(i.e., сравниваются длины) или, в случае 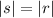 , если
, если  лексикографически
предшествует
лексикографически
предшествует  . Т.о., все программы можно отсортировать относительно
. Т.о., все программы можно отсортировать относительно 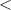 , получив в результате
упорядоченную последовательность
, получив в результате
упорядоченную последовательность 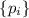 . Будем считать, что для любой программы
. Будем считать, что для любой программы 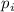 можно
построить специализированное вычислительное устройство
можно
построить специализированное вычислительное устройство 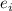 , преобразующее входные данные
, преобразующее входные данные  в
выходные
в
выходные 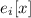 (эта нотация, по-факту, означает запуск устройства
(эта нотация, по-факту, означает запуск устройства 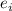 с аргументом
с аргументом  ).
).
Теперь можно определить функцию 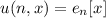 . Полнота по Тьюрингу позволяет утверждать, что
для любой вычислимой функции
. Полнота по Тьюрингу позволяет утверждать, что
для любой вычислимой функции 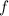 существует вычислительное устройство
существует вычислительное устройство  , такое, что
, такое, что 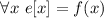 ; а раз в последовательности
; а раз в последовательности 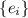 есть вычислительные устройства для всех
программ, то найдётся число
есть вычислительные устройства для всех
программ, то найдётся число 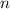 , такое, что
, такое, что 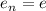 . Получается, что
. Получается, что 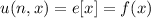 , т.е.,
функция
, т.е.,
функция  может использоваться вместо любой вычислимой функции
может использоваться вместо любой вычислимой функции 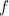 если известен её номер
если известен её номер 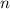 ;
другими словами,
;
другими словами,  – универсальная функция.
– универсальная функция.
Осталось показать, что  вычислима. Для этого надо написать интерпретатор
вычислима. Для этого надо написать интерпретатор 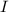 и сконструирвать
соответствующее вычислительное устройство
и сконструирвать
соответствующее вычислительное устройство 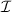 , по первому аргументу
, по первому аргументу 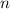 командной
строки извлекающее устройство с индексом
командной
строки извлекающее устройство с индексом 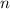 из последовательности
из последовательности 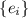 и запускающее его,
передавая ему при запуске остальные свои аргументы. Т.е., должно выполняться
и запускающее его,
передавая ему при запуске остальные свои аргументы. Т.е., должно выполняться 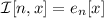 . Видно, что
. Видно, что 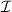 – устройство, вычисляющее
– устройство, вычисляющее  , а
, а 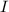 – программа, это
делающая. Таким образом,
– программа, это
делающая. Таким образом,  – вычислимая универсальная функция.
– вычислимая универсальная функция. 
N.B., сама теорема не зависит от языка программирования и требует лишь его полноты по Тьюрингу, т.е. возможности написать для любой вычислимой функции программу, её вычисляющую; да, звучит немного тавтологично, и, тем не менее, есть языки не являющиеся Тьюринг-полными: на них нельзя реализовать некоторые программы, легко пишущиеся на каком-нибудь универсальном, Тьюринг-полном языке. Существуют ли программы, не могущие быть перенесены на машину Тьюринга или любую эквивалентную ей машину, но могущие выполняться на каком-нибудь другом компьютере – интересный философский вопрос; тезис Чёрча-Тьюринга говорит, что нет, таких программ не существует (и действительно, все известные теоретические конструкции более мощных компьютеров конфликтуют с теми или иными физическими законами и в это вселенной работать не могут).
А вот существование вычислимой универсальной функции, по-видимому, не влечёт за собой полноты по Тьюрингу – если взять некоторый подходящий неуниверсальный язык, то можно действовать как в вышеприведенном наброске доказательства, т.е. можно сгенерировать и отсортировать все программы [для этого языка] и вычислительные устройства, а потом определить функцию, выбирающую и использующую нужное устройство по его номеру. Если выбранный язык будет достаточно богат, чтобы на нём можно было выразить такой выбор и запуск, то мы получим вычислимую универсальную функцию, правда, универсальную не для всех вычислимых функций, а только для функций, реализуемых на таком языке.
Фактически, теорема об универсальной функции говорит, что частичная (т.е. не являющаяся всюду
определённой) функция 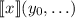 от аргументов
от аргументов 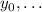 сама
является вычислимой (или т.н. частично рекурсивной) функцией
сама
является вычислимой (или т.н. частично рекурсивной) функцией 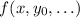 от аргументов
от аргументов
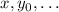 (добавился ещё один аргумент).
(добавился ещё один аргумент).
Использование теоремы об универсальной функции в данном сообщении будет весьма ограниченным;
здесь без неё можно было бы и обойтись (если не считать теорему Роджерса, см. ниже). И всё-же
она в определённые моменты будет важна. Кроме этого, стоит обратить внимание на использованное в
доказательстве разделение на программы (тексты программ), вычислительные устройства и их номера,
– нам пришлось использовать устройства, чтобы подчеркнуть механистичность и физическую
реализуемость вычислений, текстовое представление программ, чтобы иметь возможность сортировать
и нумеровать программы/устройства, и, наконец, пришлось выбрать конкретный (но не единственный)
способ такой нумерации с помощью сортировки по возрастанию относительно порядка 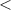 .
.
В дальнейшем такое разделение представлений будет лишним и поэтому, как я уже говорил ранее,
тексты программ, программы и их номера будут отождествляться. Сам конкретный способ нумерации
можно будет считать заданием языка программирования, хотя на практике же удобно отождествлять
язык программирования с семантической функцией 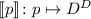 ,
сопоставляющей программе
,
сопоставляющей программе 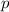 функцию
функцию  , где
, где 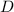 – множество, над которым определены
вычислимые функции (в большинстве случаев можно считать
– множество, над которым определены
вычислимые функции (в большинстве случаев можно считать 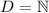 ) или с парой
) или с парой 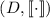 . (В следующей части этой серии сообщений, я постараюсь уделить
должное внимание понятию нумерации, но здесь оно свою полезность, похоже, пока исчерпало.)
. (В следующей части этой серии сообщений, я постараюсь уделить
должное внимание понятию нумерации, но здесь оно свою полезность, похоже, пока исчерпало.)
N.B., Также подразумевается, что паре значений 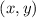 можно сопоставить взаимно однозначным
образом
можно сопоставить взаимно однозначным
образом 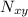 (причем отображение
(причем отображение 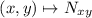 вычислимо). Это позволяет определять
функции с большим количеством аргументов через функции с меньшим количеством, например
вычислимо). Это позволяет определять
функции с большим количеством аргументов через функции с меньшим количеством, например
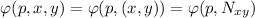 . Т.о., теоретически можно вообще
обходиться только одноместными функциями, но из соображений удобства, к такому минимализму
прибегать, надеюсь, не придётся.
. Т.о., теоретически можно вообще
обходиться только одноместными функциями, но из соображений удобства, к такому минимализму
прибегать, надеюсь, не придётся.
S-m-n теорема Клини
Другой, не менее важной теоремой является т.н. 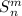 -теорема (известная также как теорема о
параметризации или итеративная теорема) [14, 3], утверждающая, что может быть написана
программа, уменьшающая количество аргументов путем фиксации значений некоторых из них: для
программы
-теорема (известная также как теорема о
параметризации или итеративная теорема) [14, 3], утверждающая, что может быть написана
программа, уменьшающая количество аргументов путем фиксации значений некоторых из них: для
программы 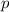 , реализующей функцию
, реализующей функцию 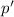 с
с 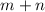 аргументами и для заданных значений
аргументами и для заданных значений
 для первых
для первых 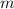 аргументов существует программа
аргументов существует программа 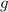 для специализированной
для специализированной
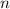 -местной функции, удовлетворяющая
-местной функции, удовлетворяющая 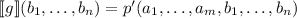 для любых
для любых 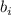 .
.
Также существует вычислимая (примитивно рекурсивная при определённом выборе языка
программирования) всюду определённая функция, — собственно, 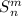 -функция, — преобразующая
программу
-функция, — преобразующая
программу 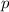 в программу
в программу 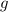 .
.
То есть, для программы 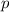 выполняется
выполняется 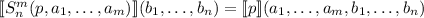 .
.
Далее пригодится частный случай 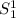 с фиксацией всего одного из двух аргументов.
с фиксацией всего одного из двух аргументов.
Нетрудно видеть, что 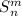 теорема, по-существу, реализует частичные вычисления (специализацию
программ) [4, 5], т.е. дает возможность выполнить часть вычислений, зависящих от фиксируемого
аргумента(-ов), заранее, до выполнения программы (что может быть использовано, например, для
оптимизации кода). Есть некоторое сходство между частичной специализацией и каррингом из
функционального программирования.
теорема, по-существу, реализует частичные вычисления (специализацию
программ) [4, 5], т.е. дает возможность выполнить часть вычислений, зависящих от фиксируемого
аргумента(-ов), заранее, до выполнения программы (что может быть использовано, например, для
оптимизации кода). Есть некоторое сходство между частичной специализацией и каррингом из
функционального программирования.
Доказательство 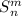 теоремы конструктивно и может быть основано на явном выписывании
программы (или на явном построении машины Тьюринга), присваивающей определенные значения
исключаемым аргументам и обеспечивающей запуск программы при поступлении недостающих данных
(такого тривиального алгоритма недостаточно для написания оптимизирующего специализатора; но он
может быть улучшен).
теоремы конструктивно и может быть основано на явном выписывании
программы (или на явном построении машины Тьюринга), присваивающей определенные значения
исключаемым аргументам и обеспечивающей запуск программы при поступлении недостающих данных
(такого тривиального алгоритма недостаточно для написания оптимизирующего специализатора; но он
может быть улучшен).
(Само доказательство здесь приводится не будет, а интересующимся рекомендуется обратиться к первоисточникам или более современным материалам по теории вычислимости.)
Стоит отметить, что вышеприведенные теоремы во многом схожи, и даже в некотором смысле
«взаимо-обратны» – теорема об универсальной функции преобразует «статический» параметр —
программу — в «динамический» аргумент, который может затем принимать любое значение;
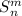 -теорема, напротив, преобразует динамический аргумент в статический, приписывая ему
априори заданное значение.
-теорема, напротив, преобразует динамический аргумент в статический, приписывая ему
априори заданное значение.
Эта симметрия хорошо видна если выписать ключевые уравнения обоих теорем одно под другим
(здесь, для краткости, используется 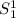 -функция):
-функция):
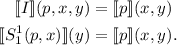
В некотором смысле, они при этом всё-же различны – кроме структурных различий формул,
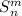 -функцию можно считать примитивно рекурсивной (для её реализации не обязательно нужен
универсальный язык программирования).
-функцию можно считать примитивно рекурсивной (для её реализации не обязательно нужен
универсальный язык программирования).
Неподвижные точки вычислимых функций
Далее описывается теорема о существовании неподвижных точек вычислимых функций, известная также как вторая рекурсивная теорема Клини [14]; здесь приводится несколько упрощенная её версия, впрочем, полностью достаточная для решения поставленных задач.
Вторая рекурсивная теорема Клини.
Для любой вычислимой функции 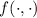 существует программа
существует программа 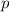 («неподвижная точка»),
такая, что
(«неподвижная точка»),
такая, что

Доказательство.
Напишем программу  , такую, что
, такую, что 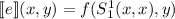 . Тогда
. Тогда
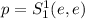 .
.
Действительно, если запустим 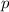 для какого-нибудь аргумента
для какого-нибудь аргумента  , то получим
, то получим 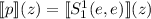 . По определению
. По определению 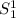 -функции,
-функции, 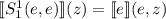 . Теперь применим определение для
. Теперь применим определение для  и
получим, что
и
получим, что 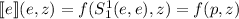 . Понятно, что эта цепочка
равенств по транзитивности приводит к
. Понятно, что эта цепочка
равенств по транзитивности приводит к 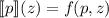 .
. 
В данном сообщении особый интерес представляет частный случай 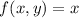 , порождающий квайны:
легко видеть, что при этом
, порождающий квайны:
легко видеть, что при этом 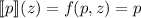 , то есть программа
, то есть программа 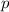 при
запуске печатает сама себя, как и положено квайну.
при
запуске печатает сама себя, как и положено квайну.
Иногда пригождается другая версия этой теоремы (при определенном выборе языка, строго говоря, не эквивалентная теореме Клини; см. [39]), предложенная в [19]:
Теорема Роджерса.
Для любой всюду определённой вычислимой функции 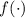 существует неподвижная точка
существует неподвижная точка 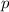 ,
т.е. такая программа
,
т.е. такая программа 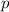 , что
, что 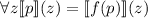 .
.
Доказательство.
Определим функцию 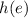 так, что
так, что

Теперь напишем программу
 , такую, что
, такую, что 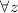 выполняется
выполняется 
Утверждается, что
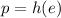 – есть искомая неподвижная точка.
– есть искомая неподвижная точка.
Подстановка (3) в правую часть (2) дает 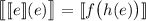 и
и 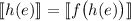 . Последнее уравнение при обозначении
. Последнее уравнение при обозначении
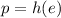 уже соответствует определению неподвижной точки из условия этой теоремы, т.е.,
уже соответствует определению неподвижной точки из условия этой теоремы, т.е.,
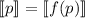 .
. 
N.B., во второй теореме Клини о рекурсии мы можем выбрать любую вычислимую функцию 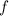 , даже
если она не определена для некоторых значений аргументов (т.е. если соответствующая этой функции
программа зависает при таких входных данных); в теореме Роджерса мы можем выбрать только всюду
определённую функцию
, даже
если она не определена для некоторых значений аргументов (т.е. если соответствующая этой функции
программа зависает при таких входных данных); в теореме Роджерса мы можем выбрать только всюду
определённую функцию 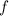 , иначе в выражении
, иначе в выражении 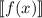 не было бы смысла при
некоторых
не было бы смысла при
некоторых  .
.
Из теоремы Клини и теоремы об универсальной функции следует теорема Роджерса, а из теоремы
Роджерса и 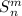 -теоремы – теорема Клини. (Но есть нюансы [39].)
-теоремы – теорема Клини. (Но есть нюансы [39].)
Для применения теоремы Роджерса к случаю с квайнами, удобно, следуя [2], ввести оператор
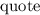 , для данного аргумента конструирующий программу, печатающую этот
аргумент. Т.е. определение оператора
, для данного аргумента конструирующий программу, печатающую этот
аргумент. Т.е. определение оператора 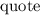 выглядит как
выглядит как
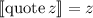 [и почти соответствует одноименному оператору из,
e.g., lisp’а].
[и почти соответствует одноименному оператору из,
e.g., lisp’а].
Квайны суть неподвижные точки этого оператора [в смысле формулировки теоремы Роджерса].
Доказательство.
Пусть 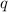 – неподвижная точка
– неподвижная точка 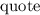 , т.е.
, т.е. 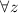 выполняется
выполняется
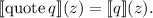 Подстановка
определения
Подстановка
определения 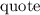 в это уравнение дает
в это уравнение дает 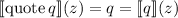 . Но
. Но 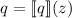 и есть определение
квайна.
и есть определение
квайна. 
Примечание.
Вообще, в математике, неподвижной точкой функции 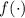 обычно называют значение
обычно называют значение
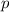 , такое, что
, такое, что 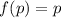 (i.e.,
(i.e., 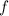 оставляет
оставляет 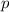 неизменным). Поэтому «неподвижные точки» из
теорем 1 и 2 не совсем соответствуют такому общепринятому определению.
неизменным). Поэтому «неподвижные точки» из
теорем 1 и 2 не совсем соответствуют такому общепринятому определению.
Тем не менее, термин неподвижная точка хорошо отражает суть этих теорем – некоторое
преобразование не меняет значение аргумента, т.е. оставляет его неподвижным (более того, из
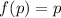 следует
следует 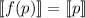 , i.e. неподвижные точки по
Роджерсу очень близки к обычному определению; обратное, впрочем, неверно: рассмотренные теоремы
о неподвижной точке вовсе не гарантируют наличия обычной неподвижной точки
, i.e. неподвижные точки по
Роджерсу очень близки к обычному определению; обратное, впрочем, неверно: рассмотренные теоремы
о неподвижной точке вовсе не гарантируют наличия обычной неподвижной точки 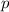 , такой, что
, такой, что
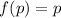 ).
).
Я лишь намереваюсь, в рамках этой серии сообщений, для удобства ввести обозначения для этих
«нестандартных» неподвижных точек, а именно, пусть операторы 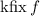 и
и
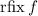 обозначают неподвижные точки [функции
обозначают неподвижные точки [функции 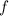 ] из теорем Клини и Роджерса,
соответственно. В контексте, требующем работы с несколькими неподвижными точками, эти операторы
будут обозначать множества неподвижных точек. Обозначение
] из теорем Клини и Роджерса,
соответственно. В контексте, требующем работы с несколькими неподвижными точками, эти операторы
будут обозначать множества неподвижных точек. Обозначение 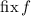 будет
использоваться для множества традиционных неподвижных точек,
будет
использоваться для множества традиционных неподвижных точек, 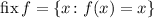 . А так как, в общем случае, неподвижная точка не является единственной, запись типа
. А так как, в общем случае, неподвижная точка не является единственной, запись типа
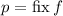 пусть означает
пусть означает 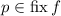 (и аналогично для
(и аналогично для
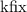 ,
, 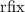 ).
).
Финальное замечание, полностью оправдывающее название «неподвижная точка» для операторов
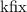 и
и 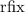 : введем оператор
: введем оператор 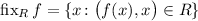 , где
, где 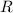 – некоторое двуместное отношение. Тогда
– некоторое двуместное отношение. Тогда
 . Другие типы неподвижных точек можно теперь тоже
определять через
. Другие типы неподвижных точек можно теперь тоже
определять через 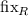 при должном выборе отношения
при должном выборе отношения 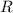 . Например, пусть
отношение
. Например, пусть
отношение  сравнивает программы по их эффекту, т.е.,
сравнивает программы по их эффекту, т.е.,
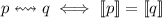 . Тогда
. Тогда
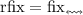 . (N.B., как обычно, запись
. (N.B., как обычно, запись
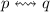 есть сокращение для
есть сокращение для 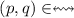 ).
).
Главный эксперимент
В [42] приведен следующий эксперимент по квайногенерации на lisp (автор кода мне не известен):
(define g (quote (lambda (x y) x))) ; g(x, y) = x
(define s11 (quote (lambda (f x) (list (quote lambda)
(quote (y)) (list f x (quote y)))))) ; from s-m-n theorem
(define m (list (quote lambda) (quote (x y))
(list g (list s11 (quote x) (quote x)) (quote y))))
(define quine (eval (list s11 m m)))
; tests
(eval (list quine nil))
(eval (list g quine nil))
(В [47] можно найти невероятную коллекцию аналогичных экспериментов со второй рекурсивный теоремой Клини, выполненных на языке scheme, диалекте lisp’а.)
Этот фрагмент кода просто воспроизводит доказательство второй рекурсивной теоремы Клини.
Аналогичным образом я действовал и при повторении этого эксперимента на sed. Соответствующий код
может быть найден в GitHub-репозитории [46]. Конкретно, в репозитории содержится ряд скриптов,
*.sed и *.sh, назначение каждого из которых рассмотренно ниже.
Редактор sed направляет данные со стандартного ввода в основной буфер редактирования (т.н. the pattern space). И т.к. мне не известен способ передачи традиционных аргументов командной строки скрипту для этого редактора, то именно чтение со стандартного ввода было применено в качестве единственного механизма передачи аргументов. При этом, из-за необходимости передачи нескольких аргументов, понадобилось либо ввести разделитель/терминатор (e.g. нулевой байт), либо приписывать значение длины перед каждым аргументом. Как ни странно, изначально был выбран второй метод, в основном из-за отсутствия необходимости в экранировании разделителя.
Итак, далее приведен перечень скриптов с их кратким описанием:
-
construct-input.shпринимает на вход список файлов со значениями аргументов и формирует пакет аргументов из них, т.е. читает эти значения и посылает на стандартный вывод, снабдив заголовками (длинами). Формат пакета данных с аргументами выглядит так:<длина аргумента 1>...<длина аргумента n><аргумент 1>...<аргумент n>Длина каждого аргумента представлена двоичным шестнадцатиразрядным числом (т.е. этот формат не отличается универсальностью, но этого хватает для практического применения).
-
Скрипт
s11.sed[тривиально] реализует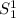 -функцию. Этот сценарий принимает исходную
программу
-функцию. Этот сценарий принимает исходную
программу 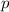 в первом аргументе и фиксируемый аргумент
в первом аргументе и фиксируемый аргумент  для неё – во втором своем
аргументе. Результатом работы скрипта будет другая программа, полученная путем приписывания к
для неё – во втором своем
аргументе. Результатом работы скрипта будет другая программа, полученная путем приписывания к
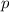 небольшого «инъектора» – фрагмента кода, встраивающего ранее принятый аргумент
небольшого «инъектора» – фрагмента кода, встраивающего ранее принятый аргумент  (и
теперь являющийся частью инъектора) перед новым аргументом
(и
теперь являющийся частью инъектора) перед новым аргументом 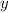 (который будет передан
формируемой программе при её запуске). После модификации пакета аргументов, инъектор передаёт
управление программе
(который будет передан
формируемой программе при её запуске). После модификации пакета аргументов, инъектор передаёт
управление программе 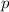 так, что она «видит» пару аргументов
так, что она «видит» пару аргументов  и
и 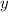 , несмотря на то,
что при запуске ей был передан единственный аргумент
, несмотря на то,
что при запуске ей был передан единственный аргумент 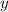 .
.Небольшая техническая сложность заключается в необходимости экранирования специальных символов в аргументе
 при формировании инъектора (с
при формировании инъектора (с  , встроенным в него). Экранирование
производится в соответствии с синтаксисом регулярных выражений sed, путем добавления
символа
, встроенным в него). Экранирование
производится в соответствии с синтаксисом регулярных выражений sed, путем добавления
символа\перед некоторыми символами, вроде того же\или перевода строки\n. -
minifier.sedиспользуется для удаления ненужных символов (пустые строки, комментарии). При генерации квайна этот скрипт применяется для опционального «сжатия» скриптовs11.sedиduplicate-first.sed, что впоследствии уменьшает размер и увеличивает скорость работы результирующего квайна. -
is-quine.sh– простой shell-скрипт, проверяющий переданный ему в аргументах sed-скрипт и определяющий, является ли он квайном. -
generate.shпроизводит «минификацию» скриптовs11.sedиduplicate-first.sed, после чего запускаетgenerate-q.sh, а после его завершения проверяет готовый продукт — квайн в файлеq.sed— с помощью скриптаis-quine.sh -
duplicate-first.sedпринимает два аргумента и
и 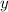 и заменяет второй первым, т.е.,
игнорирует
и заменяет второй первым, т.е.,
игнорирует 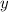 и формирует пакет из двух одинаковых аргументов
и формирует пакет из двух одинаковых аргументов  и
и  .
. -
generate-e.shконструирует программу из доказательства теоремы Клини. Для этого
[минифицированный, сжатый] код программы
из доказательства теоремы Клини. Для этого
[минифицированный, сжатый] код программы duplicate-first.sedдобавляется в начало [тоже сжатого]s11.sedи объединённый код сохраняется вe.sed. При запуске , как и
требуется, будет выполняться
, как и
требуется, будет выполняться 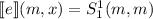 , т.е. сначала
второй аргумент будет заменен первым (с помощью кода из
, т.е. сначала
второй аргумент будет заменен первым (с помощью кода из duplicate-first.sed), затем управление будет передано коду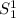 -функции из
-функции из s11.sed. -
generate-q.shсначала запускаетgenerate-e.shдля созданияe.sed, потом запускаетs11.sed(или его сжатую версию, хотя здесь это не имеет значения) передав ему в качестве обоих его аргументов содержимое только что сгенерированногоe.sed. (N.B.,generate-e.shиспользовал содержимоеs11.sedдля генерацииe.sedна его основе; в данном же случае, скриптуgenerate-q.shне требуется доступ к текстуs11.sed, но лишь возможность его выполнения; по той же причине здесь не используетсяduplicate-first.sed) -
first-only.sedиз двух переданных ему аргументов возвращает только первый. Реализует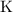 -комбинатор из комбинаторной логики и
-комбинатор из комбинаторной логики и 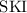 -исчисления. В
дистрибутив/репозиторий включен просто для демонстрации, хотя, в соответствии с
доказательством теоремы Клини, является реализацией функции
-исчисления. В
дистрибутив/репозиторий включен просто для демонстрации, хотя, в соответствии с
доказательством теоремы Клини, является реализацией функции 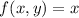 , позже
использовавшейся для доказательства существования квайна.
, позже
использовавшейся для доказательства существования квайна. -
concat.sedвозвращет объединённые значения обоих аргументов; никакие заголовки в результат не включаются. На деле,concat.sedвключен в репозиторий только для демонстрации – скриптgenerate-e.shне используетconcat.sed, а производит объединение текстов просто последовательным копированием оных в целевой файл.
(Заметьте, последние два скрипта, first-only.sed и concat.sed концептуально не являются
лишними и они могли бы быть использованы, но по-факту, в ходе оптимизации, были заменены
аналогичными средствами командной оболочки, – для эффективности.)
Для генерации квайна достаточно запустить ./generate.sh, в результате чего в том же каталоге
[через некоторое время] должен появиться файл q.sed, являющийся искомым квайном на sed.
Промежуточные итоги
Описание основного эксперимента завершено (и я рекомендую немного поизучать код скриптов из репозитория). Но о квайнах рассказать можно ещё многое. А некоторые вопросы остаются вовсе малоизученными, фактически, открытыми.
Несмотря на приведенные доказательста теорем о неподвижных точках (Клини и Роджерса), кому-то, может быть, хотелось бы глубже понять структуру этих и подобных им доказательств. Поэтому ниже я приведу некоторые дополнительные сведения с примерами. К концу сообщения я попробуя немного задеть некоторые из философских аспектов квайнов и теории вычислимости. И, пожалуй, завершу изложение попыткой сформулировать интересующие меня, но пока не имеющие официального ответа открытые вопросы.
Надеюсь, это не последнее сообщение этой серии. Поэтому, темы, не затронутые здесь, будут, по возможности, обсуждаться позже в других частях.
Дополнительная теория
Проблема остановки
Проблемой останова(-ки) называют задачу определения завершаемости произвольной программы по её коду. Известна теорема об алгоритмической неразрешимости такой задачи, т.е. о невозможности построения алгоритма, устанавливающего для произвольной программы конечность времени её выполнения [8].
Доказательство 1.
В пользу этого утверждения можно привести такие доводы. Введем функцию 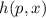 , определённую
для всех
, определённую
для всех 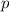 , которая в качестве своих аргументов принимает текст некоторой программы
, которая в качестве своих аргументов принимает текст некоторой программы 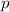 и
входные данные
и
входные данные  этой программы, после чего возвращает 1 если эта программа завершается за
конечное время, и 0 – если программа «зависает»:
этой программы, после чего возвращает 1 если эта программа завершается за
конечное время, и 0 – если программа «зависает»:
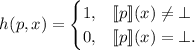
Пусть 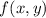 – любая вычислимая (реализуемая в виде компьютерной программы) функция двух
аргументов, способная обрабатывать тексты программ. Напишем программу
– любая вычислимая (реализуемая в виде компьютерной программы) функция двух
аргументов, способная обрабатывать тексты программ. Напишем программу 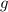 так, чтобы
выполнялось:
так, чтобы
выполнялось:
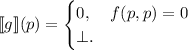
Т.е. 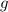 передаёт свой аргумент функции
передаёт свой аргумент функции 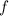 и если та возвращает ноль, то ноль (или любое другое
конечное значение) возвращает и
и если та возвращает ноль, то ноль (или любое другое
конечное значение) возвращает и 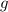 , но в противном случае
, но в противном случае 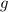 возвращает неопределенное
значение, а именно зависает, входя в бесконечный цикл.
возвращает неопределенное
значение, а именно зависает, входя в бесконечный цикл.
Так как 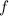 тоже реализуема в виде программы (т.е. вычислима), то получение значения
тоже реализуема в виде программы (т.е. вычислима), то получение значения 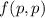 можно считать обычным вызовом подпрограммы. Все остальные действия (проверка на равенство нулю,
возврат результата, условный переход, бесконечный цикл) тоже выполнимы на любом комппьютере.
можно считать обычным вызовом подпрограммы. Все остальные действия (проверка на равенство нулю,
возврат результата, условный переход, бесконечный цикл) тоже выполнимы на любом комппьютере.
Теперь мы можем передать программе 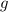 её собственный текст; тогда, если
её собственный текст; тогда, если 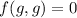 , то и
, то и
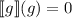 . Другими словами, в этом случае
. Другими словами, в этом случае 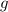 возвращает результат и
завершается, т.е.
возвращает результат и
завершается, т.е. 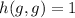 . Если же
. Если же 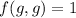 , то
, то 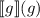 зависает и
таким образом
зависает и
таким образом 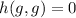 .
.
В любом случае, из этого получается, что 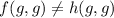 . Таким образом, функция
. Таким образом, функция 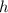 не
совпадает [хотя бы в одной точке] с вычислимой
не
совпадает [хотя бы в одной точке] с вычислимой 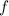 . А из произвольности выбора функции
. А из произвольности выбора функции 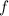 немедленно вытекает, что функция
немедленно вытекает, что функция 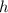 не совпадает вообще ни с одной вычислимой функцией, т.е.
не совпадает вообще ни с одной вычислимой функцией, т.е.
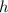 невычислима (в смысле несуществования программы, вычисляющей значение этой функции для всех
программ).
невычислима (в смысле несуществования программы, вычисляющей значение этой функции для всех
программ). 
Доказательство 2.
Интересно, что можно воспользоваться теоремой Клини и попробовать доказать проблему останова методом «от противного».
Допустим, определённая выше функция останова 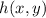 – вычислимая. Определим вычислимую
функцию
– вычислимая. Определим вычислимую
функцию
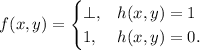
Вторая рекурсивная теорема говорит, что
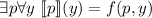 . Определение
равенства вычислимых функций, определение
. Определение
равенства вычислимых функций, определение 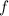 и определение функции останова дают следующие
цепочки логических эквавалентностей
и определение функции останова дают следующие
цепочки логических эквавалентностей 
Пришли к противоречию; значит, функция
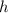 не является вычислимой.
не является вычислимой. 
Диагонализация
Схема первого доказательства для проблемы останова фактически основана на процедуре
диагонализации [6]. Второе доказательство, впрочем, тоже: ведь оно использует теорему Клини,
доказательство которой также основано на диагонализации. Далее я попытаюсь пояснить суть этого
процесса. Итак, если у нас есть некоторая бесконечная матрица 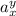 (верхний индекс нумерует
строки, нижний – столбцы), то мы можем построить вектор-строку
(верхний индекс нумерует
строки, нижний – столбцы), то мы можем построить вектор-строку 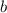 , не совпадающий ни с одной
из строк матрицы. Для этого достаточно лишь каким-то образом преобразовать элементы диагонали
(отсюда название метода) матрицы
, не совпадающий ни с одной
из строк матрицы. Для этого достаточно лишь каким-то образом преобразовать элементы диагонали
(отсюда название метода) матрицы  так, чтобы для любого
так, чтобы для любого  выполнялось
выполнялось 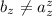 (например,
(например, 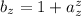 ).
).
Действительно, предположим, что 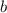 равен одной из строк матрицы
равен одной из строк матрицы  . Это означает, что
существует такой индекс
. Это означает, что
существует такой индекс  , что
, что 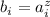 для всех
для всех  . Однако, по-построению
. Однако, по-построению 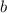 , при
, при
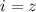 имеет место неравенство
имеет место неравенство 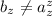 ; противоречие. Следовательно, мы действительно
построили новый объект
; противоречие. Следовательно, мы действительно
построили новый объект 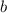 , не входящий в матрицу
, не входящий в матрицу  .
.
Примечание.
Название метода (диагонализация) несколько условно, т.к., по-видимому, достаточно чтобы в каждой строке был хотя-бы один преобразуемый элемент, совсем не обязательно лежащий на главной диагонали. [44] (Правда, нужно учитывать, что перестановкой строк можно вернуть преобразуемые элементы на диагональ матрицы; это замечание пока имеет интуитивный характер и детального анализа здесь не будет.)
Возможно, что пока применение этого трюка с конструированием патологической строки матрицы может показаться далёким от приведенных доказательств разбираемых здесь теорем (Клини, Роджерса и проблемы остановки); поэтому представляется нелишним небольшое продвижение ближе к историческим основам метода, и, я надеюсь, это сразу прояснит связь по крайней мере с проблемой останова. А вот теоремы о неподвижных точках потребуют большего внимания… Итак, сейчас копнём вглубь истории.
Теорема Кантора
Изначально, диагональный метод был разработан и применен Кантором [7] для доказательства
существования множеств, больших любого счетного бесконечного множества, или, точнее говоря, для
доказательства несуществования сюръекции 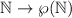 , где
, где 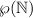 – булеан множества
– булеан множества 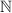 . Можно выразить теорему Кантора так:
. Можно выразить теорему Кантора так:
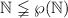 . В более общем виде, теорема Кантора говорит о несуществовании
сюръекции
. В более общем виде, теорема Кантора говорит о несуществовании
сюръекции 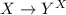 , где
, где 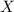 ,
, 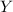 – некоторые множества (причем
– некоторые множества (причем 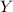 должно быть невырожденным,
например в смысле существования беспорядка
должно быть невырожденным,
например в смысле существования беспорядка  , т.е., перестановки без неподвижных точек),
а
, т.е., перестановки без неподвижных точек),
а 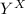 – множество всех функций
– множество всех функций 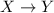 (структурно, обозначение
(структурно, обозначение 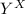 соответствует формуле
соответствует формуле
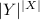 для подсчета количества таких функций).
для подсчета количества таких функций).
Рассмотрим более детально пример с 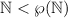 .
.
Мы можем закодировать произвольное подмножество  двоичной маской, т.е.
последовательностью
двоичной маской, т.е.
последовательностью 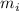 , такой, что
, такой, что 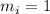 если
если 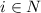 и
и 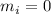 если
если 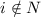 .
.
После этого мы сможем определить матрицу 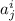 (бесконечных размеров), каждая строка
(бесконечных размеров), каждая строка 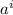 которой будет содержать двоичную маску для каждого подмножества
которой будет содержать двоичную маску для каждого подмножества 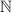 . Теперь мы применим
к диагональным элементам
. Теперь мы применим
к диагональным элементам 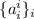 матрицы операцию инвертирования
матрицы операцию инвертирования 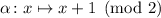 (т.е.
(т.е. 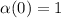 и
и 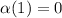 ), в результате чего получим новый
бесконечный вектор-строку
), в результате чего получим новый
бесконечный вектор-строку 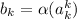 , который не будет совпадать ни с одной из строк
матрицы.
, который не будет совпадать ни с одной из строк
матрицы.
Т.е. мы получили совершенно новый объект, имеющий конкретное описание в виде двоичной
последовательности, тоже могущей быть двоичной маской для некоторого подмножества 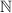 ,
но не входящей в матрицу
,
но не входящей в матрицу  . Этот пример показывает, что раз строки матрицы пронумерованы
числами
. Этот пример показывает, что раз строки матрицы пронумерованы
числами 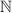 , а мы получили «лишнюю» двоичную маску, определяющую некое «лишнее»
подмножество
, а мы получили «лишнюю» двоичную маску, определяющую некое «лишнее»
подмножество 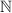 , то множество всех подмножеств
, то множество всех подмножеств 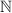 , содержащее это лишнее
подмножество и обозначаемое
, содержащее это лишнее
подмножество и обозначаемое 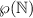 , строго больше самого
, строго больше самого 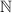 ; выражение
«строго больше» означает, что в
; выражение
«строго больше» означает, что в 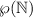 есть лишние, дополнительные элементы и
нельзя определить какую-нибудь функцию из
есть лишние, дополнительные элементы и
нельзя определить какую-нибудь функцию из 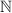 на
на 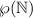 , т.е. такую
функцию, чтобы у каждого элемента
, т.е. такую
функцию, чтобы у каждого элемента 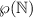 был прообраз.
был прообраз.
Применительно же к проблеме останова, в качестве бесконечной матрицы используются значения 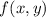 , т.е. строки соответствуют функциям. Причем диагональные значения оборачиваются в функцию
, т.е. строки соответствуют функциям. Причем диагональные значения оборачиваются в функцию
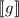 так, чтобы функция останова
так, чтобы функция останова 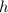 [хотя бы на диагональных элементах
матрицы] возвращала результат, отличный от результата применения
[хотя бы на диагональных элементах
матрицы] возвращала результат, отличный от результата применения 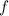 к тем же аргументам.
к тем же аргументам.
Теорема Ловера
Уильям Ловер предложил [43] обобщенную теорему из которой следуют многие другие результаты диагонализации, включая и проблему останова и теорему Гёделя о неполноте и некоторые другие. См. [44] для изложения тех же результатов на языке теории множеств (работа [43] сформулирована с существенным привлечением теории категорий).
Связь диагонализации с теоремами о неподвижной точке
(Этот подраздел добавлен через месяцы после размещения в моем дневнике первой версии этого сообщения. Добавить новый подраздел, демонстрирующий роль диагонализации при поиске неподвижных точек, я решил после того как однажды прочитал своё же сообщение и не увидел чётких следов диагонального процесса в приведенных доказательствах теорем Клини и Роджерса, кроме характерного приема с самоприменением программ… Материал в основном написан по мотивам [56].)
В рассмотренных выше примерах применения диагонального процесса мы определяли множество всех объектов определённого типа, представляли их строками матрицы, а затем применяли некоторую операцию к диагональным элементам и т.о. конструировали новый объект, не могущий быть описанным ни одной строкой матрицы. Но при поиске неподвижной точки, как в теоремах Клини и Роджерса, требуется, наоборот, построить или найти объект с требуемыми свойствами в исходном наборе, а не доказать, что его там нет. Причем же тут диагонализация?
Все дело в том, что если нам удается построить новую последовательность 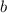 (иногда называемую
антидиагональю [ которую не следует путать с побочной диагональю матрицы]), путем применения
некоего преобразования
(иногда называемую
антидиагональю [ которую не следует путать с побочной диагональю матрицы]), путем применения
некоего преобразования 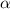 к диагональным элементам матрицы
к диагональным элементам матрицы  , то мы, как уже было
сказано ранее, можем быть уверены, что среди строк матрицы
, то мы, как уже было
сказано ранее, можем быть уверены, что среди строк матрицы  объекта
объекта 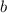 нет. Но если по
какой-то причине «антидиагональный» объект
нет. Но если по
какой-то причине «антидиагональный» объект 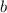 построить не получается, то среди строк матрицы
построить не получается, то среди строк матрицы
 может оказаться её диагональ. Т.е. возможно существует индекс
может оказаться её диагональ. Т.е. возможно существует индекс  , такой, что
, такой, что 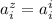 .
.
Нас интересует случай замкнутости набора строк матрицы относительно действия 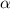 : для любой
строки
: для любой
строки 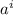 существует строка
существует строка 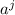 равная образу
равная образу 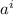 , т.е.,
, т.е., 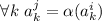 . Итак, если диагональ матрицы равна её строке
. Итак, если диагональ матрицы равна её строке 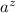 , то в силу замкнутости
строк относительно
, то в силу замкнутости
строк относительно 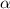 , существует строка
, существует строка 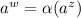 , а так как
, а так как 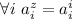 , то и образ диагонали под действием
, то и образ диагонали под действием 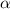 тоже оказывается среди строк:
тоже оказывается среди строк: 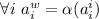 .
.
Но если результат преобразования диагонали равен одной из строк, то это означает, что на
пересечении этой строки с главной диагональю матрицы есть элемент, переходящий в себя под
действием преобразования 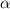 . Другими словами,
. Другими словами, 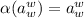 , i.e.,
, i.e., 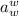 –
неподвижная точка
–
неподвижная точка 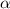 .
.
Возможно, в визуализации этой идеи поможет следующий рисунок (матрица  схематично изображена
в виде таблицы; вместо каких-либо конкретных значений её ячеек используется символ
схематично изображена
в виде таблицы; вместо каких-либо конкретных значений её ячеек используется символ  ):
):
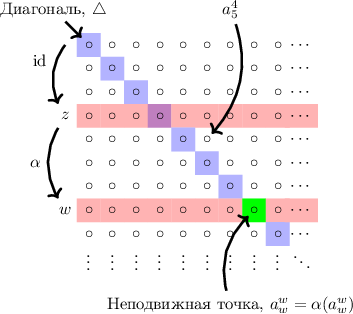
Ну вот, связь диагонализации и неподвижных точек в общих чертах продемонстрирована. Осталось
выяснить, что же может пойти не так при построении вектора 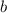 . Напомню, что в случае с теоремой
Кантора и проблемой останова диагонализация проходила успешно… Разгадка здесь всего-лишь в
том, что в случае с неподвижными точками мы не строим функцию
. Напомню, что в случае с теоремой
Кантора и проблемой останова диагонализация проходила успешно… Разгадка здесь всего-лишь в
том, что в случае с неподвижными точками мы не строим функцию 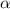 специально так, чтобы у
неё не было неподвижных точек. И лишь предполагая, допуская их наличие, мы применяем
диагональный процесс для конструирования такой неподвижной точки. Получив же конкретное решение,
можно легко убедиться, что это действительно неподвижная точка; с тем же успехом, мы могли бы
просто угадать вид решения, а потом убедиться в его правильности. Т.о., если отбросить вариант с
угадыванием, то конструктивный характер диагональной схемы существенен для её логической основы:
мы создаём объект с нужными свойствами и назад пути уже нет в силу непротиворечивости
используемых формальных систем (ведь если выведено некоторое утверждение, вывести его отрицание
в таких системах уже не получится). (Рекомендую также глянуть интересное обсуждение логической
основы диагонализации в [57].)
специально так, чтобы у
неё не было неподвижных точек. И лишь предполагая, допуская их наличие, мы применяем
диагональный процесс для конструирования такой неподвижной точки. Получив же конкретное решение,
можно легко убедиться, что это действительно неподвижная точка; с тем же успехом, мы могли бы
просто угадать вид решения, а потом убедиться в его правильности. Т.о., если отбросить вариант с
угадыванием, то конструктивный характер диагональной схемы существенен для её логической основы:
мы создаём объект с нужными свойствами и назад пути уже нет в силу непротиворечивости
используемых формальных систем (ведь если выведено некоторое утверждение, вывести его отрицание
в таких системах уже не получится). (Рекомендую также глянуть интересное обсуждение логической
основы диагонализации в [57].)
Пример приведем для теоремы Роджерса, более удобной из-за одноместности фигурирующей в ней
функции. Требуется решить уравнение 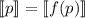 относительно
относительно 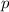 для любой всюду определённой вычислимой
для любой всюду определённой вычислимой 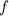 . В соответствии с вышеизложенной
схемой доказательства диагонализацией, далее предстоит определить матрицу
. В соответствии с вышеизложенной
схемой доказательства диагонализацией, далее предстоит определить матрицу  и преобразование
и преобразование
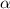 так, чтобы неподвижная точка функции
так, чтобы неподвижная точка функции 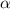 подходила бы в качестве решения к
уравнению из теоремы Роджерса.
подходила бы в качестве решения к
уравнению из теоремы Роджерса.
По техническим причинам, о которых ещё будет сказано позже, вместо функции 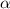 мы введем
отношение
мы введем
отношение 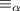 (его конкретный вид будет определён ниже). Вместо
(его конкретный вид будет определён ниже). Вместо
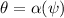 будем писать
будем писать 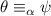 ; в частности, если некоторая
функция
; в частности, если некоторая
функция 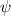 – искомая неподвижная точка, то будет выполняться
– искомая неподвижная точка, то будет выполняться 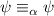 . К
строкам матрицы и вообще к последовательностям это отношение применяется поэлементно.
. К
строкам матрицы и вообще к последовательностям это отношение применяется поэлементно.
Пусть элементы матрицы равны 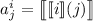 . Т.е.
строка с индексом
. Т.е.
строка с индексом  соответствует вычислимой функции с номером
соответствует вычислимой функции с номером  ; номера столбцов
соответствуют значениям аргументов. (Заметьте, что элементы матрицы
; номера столбцов
соответствуют значениям аргументов. (Заметьте, что элементы матрицы  равны не самим значениям
равны не самим значениям
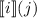 , а вычислимым функциям с номерами
, а вычислимым функциям с номерами 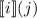 .) Если
.) Если
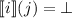 для некоторых
для некоторых  и
и 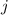 , то считается, что элемент
, то считается, что элемент 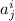 содержит нигде не определённую функцию:
содержит нигде не определённую функцию: 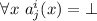 . Диагональ
. Диагональ 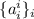 обозначим
обозначим  и будем считать
и будем считать 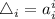 .
.
Если некоторый гипотетический объект 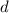 , для которого справедливо
, для которого справедливо 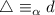 не
является «патологическим», т.е. гарантированно отсутствующим среди строк матрицы, то диагональ
может оказаться равной одной из строк.
не
является «патологическим», т.е. гарантированно отсутствующим среди строк матрицы, то диагональ
может оказаться равной одной из строк.
Мы можем определить функцию 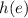 , конструирующую программу, которая принимая аргумент
, конструирующую программу, которая принимая аргумент  ,
применяет к нему диагональный элемент матрицы, находящийся на пересечении строки
,
применяет к нему диагональный элемент матрицы, находящийся на пересечении строки  и столбца
и столбца
 . А именно, выполняется
. А именно, выполняется

Важно, что для вычисления
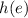 тоже можно написать программу
тоже можно написать программу  , т.е.
, т.е. 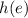 – вычислимая функция. Это
означает, что в матрице
– вычислимая функция. Это
означает, что в матрице  существует строка
существует строка 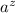 равная
равная  ; действительно, из того,
что
; действительно, из того,
что  является программой для
является программой для 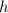 , а также из определения элементов
, а также из определения элементов 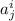 и из
и из 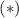 следует
следует
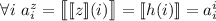 . Если набор строк замкнут относительно
. Если набор строк замкнут относительно 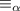 , то существует
строка
, то существует
строка 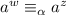 ; и именно её пересечение с
; и именно её пересечение с  дает неподвижную точку:
дает неподвижную точку:
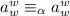 .
.
Чтобы последнее уравнение выглядело как уравнение из теоремы Роджерса, определим отношение
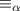 так, что для функций
так, что для функций 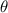 и
и 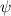 выполняется
выполняется
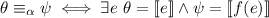 . Попробуем показать, что
. Попробуем показать, что 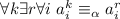 . Пусть
. Пусть 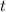 – такая последовательность, что
– такая последовательность, что 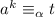 . Из определений
элементов матрицы
. Из определений
элементов матрицы  и отношения
и отношения 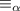 следует
следует 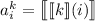 и
и 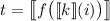 . В силу вычислимости
. В силу вычислимости 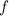 , композиция
, композиция 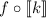 тоже вычислима и имеет некоторый индекс
тоже вычислима и имеет некоторый индекс  , т.е.,
, т.е., 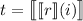 . В соответствии с определением элементов матрицы
. В соответствии с определением элементов матрицы  , это
выражение означает, что
, это
выражение означает, что 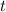 равна строке с индексом
равна строке с индексом  . Т.о., мы только что показали, что набор
строк замкнут относительно
. Т.о., мы только что показали, что набор
строк замкнут относительно 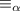 .
.
Выше было установлено, что 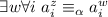 . Левую часть перепишем
с помощью
. Левую часть перепишем
с помощью 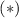 , учитывая равенство
, учитывая равенство 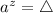 , а правую – с помощью определения элементов
матрицы
, а правую – с помощью определения элементов
матрицы  . Это даёт
. Это даёт 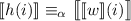 . Из определения отношения
. Из определения отношения 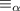 следует, что
следует, что
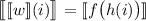 .
Это уравнение говорит, что
.
Это уравнение говорит, что 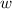 – один из возможных текстов программ, вычисляющих композицию
функций
– один из возможных текстов программ, вычисляющих композицию
функций 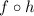 ; кроме того, то же самое уравнение вместе с
; кроме того, то же самое уравнение вместе с 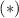 в случае с
в случае с  немедленно
даёт
немедленно
даёт 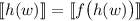 . Таким образом,
. Таким образом, 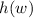 ,
где
,
где 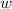 является программой для вычисления композиции
является программой для вычисления композиции 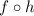 , – искомая неподвижная точка
из теоремы Роджерса, т.е.,
, – искомая неподвижная точка
из теоремы Роджерса, т.е., 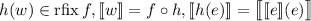 .
.
Да, это построение выглядит более громоздким и запутанным чем изначально приведенное почти однострочное доказательство теоремы Роджерса, но оно, я надеюсь, позволяет более глубоко увидеть связь диагонального процесса с теоремами о неподвижных точках.
Примечание.
Ранее я говорил, что лучше использовать отношение 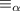 вместо функции
вместо функции 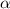 . Чтобы
неподвижная точка
. Чтобы
неподвижная точка 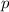 функции
функции 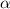 удовлетворяла уравнению
удовлетворяла уравнению 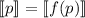 , можно было бы определить
, можно было бы определить 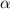 как
как 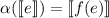 . В принципе, та же схема доказательства работала бы и в
этом случае: сначала мы бы выяснили, что строки замкнуты относительно
. В принципе, та же схема доказательства работала бы и в
этом случае: сначала мы бы выяснили, что строки замкнуты относительно 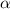 , затем
преобразовали бы строку
, затем
преобразовали бы строку 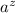 , равную диагонали
, равную диагонали  , и получили бы новую строку
, и получили бы новую строку
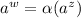 ; завершилось бы такое доказательство проверкой, что элемент
; завершилось бы такое доказательство проверкой, что элемент 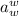 ,
находящийся на пересечении
,
находящийся на пересечении 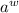 и
и  , удовлетворяет уравнению
, удовлетворяет уравнению 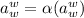 .
.
Пусть некоторый элемент в  равен
равен 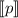 для некоторого
для некоторого 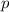 . Тогда
соответствующий элемент в
. Тогда
соответствующий элемент в 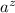 равен
равен 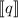 и равенство последовательностей
и равенство последовательностей
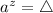 означает, что
означает, что 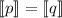 . В строке
. В строке 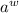 элементу
элементу 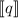 из строки
из строки 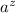 соответствует элемент
соответствует элемент 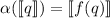 . Проблема в том, что исходный элемент
. Проблема в том, что исходный элемент 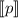 из
из  , под действием преобразования
, под действием преобразования 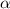 должен перейти в
должен перейти в 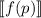 и мы вынуждены потребовать, чтобы этот результат совпадал с
и мы вынуждены потребовать, чтобы этот результат совпадал с 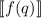 , ведь иначе нельзя будет говорить о
, ведь иначе нельзя будет говорить о 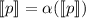 если
если 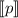 будет желаемым элементом на пересечении
будет желаемым элементом на пересечении 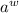 и
и
 .
.
Другими словами, из равенства 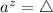 должно следовать
должно следовать 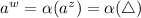 , а для этого требуется экстенсиональность функции
, а для этого требуется экстенсиональность функции 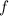 – должно выполняться
– должно выполняться
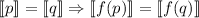 , i.e., одинаково ведущие себя программы, должны преобразовываться функцией
, i.e., одинаково ведущие себя программы, должны преобразовываться функцией 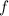 снова в одинаково себя ведущие, однако не всякая вычислимая функция обладает такой формой
монотонности. Трюк с заменой преобразования
снова в одинаково себя ведущие, однако не всякая вычислимая функция обладает такой формой
монотонности. Трюк с заменой преобразования 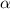 (вместе с обычным сравнением функций)
отношением
(вместе с обычным сравнением функций)
отношением 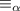 , позволяет обойти это ограничение и расширить класс пригодных функций
до всех вычислимых всюду определённых.
, позволяет обойти это ограничение и расширить класс пригодных функций
до всех вычислимых всюду определённых.
Версия «от противного».
Рассуждения по схеме «а вдруг», могут показаться не всегда удовлетворительными. Можно ли вместо попытки сконструировать желаемый объект — неподвижную точку — вопреки диагонализации (призванной доказать невозможность подобного мероприятия) попробовать облачить вышеизложенное в привычную схему доказательства от противного? Такое доказательство выглядело бы более привычно и ощущалось бы более весомым (ведь доказательство от противного основано на надёжном процессе поиска ошибки в цепочке умозаключений, приведших к абсурду; такой поиск призван, в итоге, локализовать ошибку, загнав её в единственный туманный уголок доказательства, а именно, в самое его начальное предположение, после чего способ исправления ошибки — отрицанием предположения — немедленно следует из закона исключённого третьего, и, таким образом любые претензии к качеству такого доказательства сводятся к вере в этот закон). Оказывается, что, да, доказательство, одновременно явно использующее диагонализацию и показывающее наличие неподвижной точки методом от противного, существует, и, в общем-то, общеизвестно.
Итак. Определим бинарное отношение  так, что
так, что 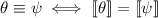 .
.
Теорема (переформулировка теоремы Роджерса).
Если 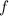 – всюду определённая вычислимая функция, то
– всюду определённая вычислимая функция, то 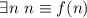 .
.
Доказательство теоремы Роджерса методом от противного.
(N.B., Акцент в этой версии доказательства сделан на диагонализации, пусть и в ущерб конструктивности, — здесь я не буду выводить явный вид неподвижной точки, хотя при желании его можно извлечь и из такой урезанной версии.)
Основное предположение: 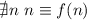 .
.
Лемма 1 (без доказательства). Для любой вычислимой функции 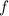 существует вычислимая всюду
определённая
существует вычислимая всюду
определённая 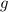 (т.н.,
(т.н.,  -продолжение функции
-продолжение функции 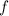 ), такая, что
), такая, что 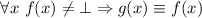 .
.
Определим вычислимую всюду определённую функцию 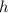 , такую, что
, такую, что 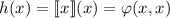 .
.
Утверждение 1. Не существует вычислимой функции 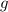 , такой, что
, такой, что 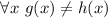 (иначе это бы противоречило определению универсальной функции
(иначе это бы противоречило определению универсальной функции 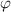 ).
).
(N.B., конкретный вид 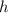 на самом деле не важен, — требуется лишь справедливость утверждения
1, — но здесь мы всё-таки зафиксируем такое «диагональное» выражение, и даже воспользуемся
им в конце этого подраздела для лучшей визуализации процесса.)
на самом деле не важен, — требуется лишь справедливость утверждения
1, — но здесь мы всё-таки зафиксируем такое «диагональное» выражение, и даже воспользуемся
им в конце этого подраздела для лучшей визуализации процесса.)
По лемме 1, 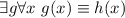 , т.е.,
, т.е., 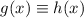 . Определим функцию
. Определим функцию
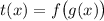 . Т.к.
. Т.к. 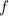 и
и 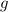 и их композиция
и их композиция 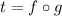 – вычислима. Допустим,
– вычислима. Допустим,
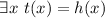 . Это вместе с
. Это вместе с 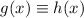 и с определением отношения
и с определением отношения  ведет
к
ведет
к 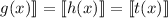 , из чего
следует
, из чего
следует 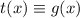 . Но
. Но 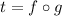 , откуда
, откуда 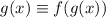 , однако по основному
предположению,
, однако по основному
предположению, 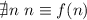 (
(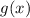 выглядит как неподвижная точка, но мы
предполагаем, что их не существует). Противоречие, значит,
выглядит как неподвижная точка, но мы
предполагаем, что их не существует). Противоречие, значит, 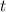 отличается всюду от
отличается всюду от 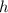 . Но это
противоречит уже утверждению 1. Следовательно, основное предположение неверно и мы
должны его исправить, заменив на
. Но это
противоречит уже утверждению 1. Следовательно, основное предположение неверно и мы
должны его исправить, заменив на 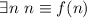 .
. 
Обратите внимание, здесь мы имеем дело с матрицей 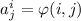 в которой строки, как и
прежде, соответствуют вычислимым функциям, а столбцы – их аргументам (изменились только сами
элементы матрицы). Функция
в которой строки, как и
прежде, соответствуют вычислимым функциям, а столбцы – их аргументам (изменились только сами
элементы матрицы). Функция 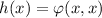 порождена диагональю
порождена диагональю 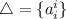 .
Лемма 1 говорит, что в матрице
.
Лемма 1 говорит, что в матрице  присутствует строка
присутствует строка 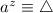 (отношение
(отношение  применено поэлементно). Мы используем эту строку для конструирования кандидата в антидиагональ,
а именно мы действуем на
применено поэлементно). Мы используем эту строку для конструирования кандидата в антидиагональ,
а именно мы действуем на 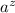 данной вычислимой функцией
данной вычислимой функцией 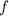 , но т.к. строка
, но т.к. строка 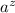 соответствует функции
соответствует функции 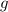 , а композиция
, а композиция 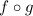 вычислима, то среди строк должна найтись
строка
вычислима, то среди строк должна найтись
строка 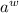 (пересекающая диагональ в некоторой точке).
(пересекающая диагональ в некоторой точке).
Откуда же тогда берутся подозрения в антидиагональности 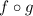 , т.е. в том, что
, т.е. в том, что 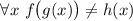 ? Мы знаем, что
? Мы знаем, что 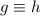 (так мы строили строку
(так мы строили строку 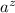 ). Теперь если
для какого-то
). Теперь если
для какого-то  верно
верно 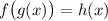 , то в строке
, то в строке 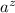 найдётся элемент
найдётся элемент 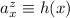 , но по определению элементов матрицы
, но по определению элементов матрицы  ,
, 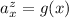 , откуда и вытекает выражение
, откуда и вытекает выражение
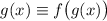 , противоречащее основному предположению [о несуществовании
неподвижной точки
, противоречащее основному предположению [о несуществовании
неподвижной точки 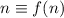 ], а значит опровергающее, методом от противного, наше
предположение о том, что
], а значит опровергающее, методом от противного, наше
предположение о том, что 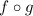 совпадает с
совпадает с 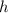 в точке
в точке  .
.
На данный момент мы имеем уже два утверждения: одно говорит о том, что антидиагональ на самом
деле равна строке 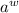 и пересекается с диагональю в некоторой точке, а второе утверждение
говорит, что антидиагональ действительно нигде не совпадает с диагональю. Эти утверждения
противоречат друг другу, что абсурдно, и, опять методом от противного, приводит к утверждению,
прямо противоположному основному предположению об отсутствии неподвижных точек у данной функции
и пересекается с диагональю в некоторой точке, а второе утверждение
говорит, что антидиагональ действительно нигде не совпадает с диагональю. Эти утверждения
противоречат друг другу, что абсурдно, и, опять методом от противного, приводит к утверждению,
прямо противоположному основному предположению об отсутствии неподвижных точек у данной функции
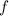 .
.
Я специально воспроизвел последнее доказательство от противного в уже знакомых терминах матриц, диагоналей, строк, антидиагоналей, и т.д., чтобы придать максимальную наглядность процессу и окончательно удалить мистический налёт с диагонального доказательства теоремы о рекурсии.
Немного о пределах познаваемости
Проблема останова разрешима для многих систем, например, для конечных автоматов, коими, кстати говоря, и являются реальные компьютеры. Правда, в силу огромного количества состояний таких автоматов, они, с практической точки зрения, хорошо моделируются машиной Тьюринга (или эквивалентными моделями, типа лямбда-исчисления). Поэтому, многие теоретические результаты, вытекающие из проблемы останова или доказываемые редукцией к ней, по прежнему применимы в обычном программировании.
Также проблема останова может быть вполне разрешимой для определенных частных случаев. Например,
в теории, антивирусы невозможны (это доказывается редукцией к проблеме остановки), но они
всё-таки вертятся существуют как программные продукты (в том числе, благодаря
«маркетингу», наверное). В теории, невозможно написать программу-детектор, безошибочно
определяющую, что другая программа печатает на экране, например, слово «привет» [28, 29]. Но
ведь многие бы без труда написали такой детектор. Даже сами доказательства теорем, в силу
соответствия Карри-Ховарда, вообще говоря, требуют решения проблемы остановки. Но ведь
математики как-то доказывают теоремы! Иногда при помощи компьютера (и автоматизированно и даже
автоматически).
Эти исключения не являются ошибками или фактами, опровергающими упомянутые контринтуитивные утверждения (содержащие квантор всеобщности). А положительные результаты имеют вполне конкретное применение. Компиляторы, интерпретаторы, квайны и многие другие интересные артефакты теории вычислимости существуют не только теоретически, но и имеют осязаемые реализации в виде реальных кусков кода и даже устройств (e.g. те же компьютеры). А теорема Гёделя о неполноте говорит, что некоторые теоремы просто не могут быть доказаны, – не стоит даже и пытаться.
Наконец, диагонализация внесла некоторый вклад и в более абстрактные области философии. Например, применением диагонального процесса к демону Лапласа — «древнему» суперкомпьютеру, имеющему неограниченный доступ к любой информации обо всех частицах вселенной — была установлена «монотеистическая» теорема о невозможности существования более чем одного демона Лапласа [27].
В следующих сообщениях этой серии я напишу о некоторых из этих [как классических, так и относительно новых] результатов подробнее.
Другие подходы и «слегка открытые» вопросы
В этом разделе обсуждаются достаточно простые, но до сих пор представляющие некоторый исследовательский интерес альтернативные подходы к конструированию квайнов. Некоторые из рассмотренных здесь вопросов могут быть тривиальными и, возможно, представляющими сложность лишь для меня; другие – могут оказаться объективно стоящими дальнейшей проработки.
Более подробно все эти воросы будет или не будут освещены в следующем(-их) сообщении(-ях) этой серии.
«Креацианизм» vs. «абиогенез»
Я условно назвал совокупность методов (как ручных, так и автоматических), применяемых для конструирования квайнов и основанных на существенном привнесении специально подготовленной внешней информации/знаний в этот процесс [квайнологическим] «креацианизмом». Традиционное написание квайна вручную, а также его конструирования на основе второй рекурсивной теоремы Клини – суть примеры креацианисткого подхода в квайнологии. В них требуется существенный контроль со стороны программиста.
В подразделах же, приведенных ниже, акцент сделан на автоматическом итеративном конструировании квайнов (если оно возможно). «Абиогенетическое», самостоятельное «зарождение» квайнов потенциально могло бы представлять некоторую ценность в ряде областей. Так, например, квайнологический абиогенез был бы интересен в таком разделе информационной безопасности как компьютерная вирусология; он был бы применим в автономных системах (e.g., самомодифицирующееся ПО каких-нибудь марсоходов) и, возможно, интересен экзобиологам (в том смысле, что квайны, будучи «дистиллированной» моделью жизни, подошли бы для изучения тварей с terra incognita, – будь-то океанские впадины, астероиды, космическая пыль/мусор, или любые другие субстраты).
Кимианские квайны и итеративное вычисление неподвижной точки
Хофштадтер в [26] не только ввел термин «квайн», но и описал там же ещё одну разновидность самореплицирующегося кода – кимианские квайны, названные в честь Скотта Кима (Scott Kim), подсказавшего эту идею Хофштадтеру.
Кимианский квайн представляет собой текст, который будучи поданым на вход компилятора/интерпретатора, не распознается как корректный исходный текст, а приводит к выводу сообщения об ошибке [31]. Причём такое сообщение побуквенно совпадает с самим кимианским квайном. Т.е. при попытке запуска или компиляции, подобный код всё-таки воспроизводит себя, как и положено квайну.
Если обозначить среду исполнения для кимианского квайна (e.g., компилятор, интерпретатор или
командную оболочку) как функцию 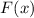 , принимающую и возвращающую текстовую строку, то
некоторый кимианский квайн
, принимающую и возвращающую текстовую строку, то
некоторый кимианский квайн 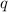 будет неподвижной точкой этой функции:
будет неподвижной точкой этой функции: 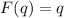 .
.
Интересно, что в данном случае 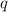 может быть вычислен итерированием функции
может быть вычислен итерированием функции 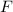 начиная с
подходящего (иногда пустого) начального приближения. Т.е. алгоритм конструирования
кимианского квайна должен будет вычислить
начиная с
подходящего (иногда пустого) начального приближения. Т.е. алгоритм конструирования
кимианского квайна должен будет вычислить 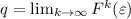 , где
, где
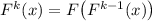 ,
, 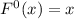 для некоторого начального значения
для некоторого начального значения  .
.
Следует заметить, что такая функция 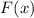 определена для всех
определена для всех  (и к тому же всегда
завершается, если речь идет о компиляторе без поддержки вычислительно-универсальных
металингвистических средств, — например, подобных C++ шаблонам, — могущих приводить к
«зависанию» компилятора).
(и к тому же всегда
завершается, если речь идет о компиляторе без поддержки вычислительно-универсальных
металингвистических средств, — например, подобных C++ шаблонам, — могущих приводить к
«зависанию» компилятора).
В минирепозитории (gist) [33] можно найти простую реализацию подобного метода итеративного конструирования кимианского квайна, выполненную на языке командной оболочки bash. Скрипт принимает в качестве аргумента путь до исполняемого файла интерпретатора или компилятора, запускает его и передает ему имя файла, хранящего начальное приближение. Результат из потоков вывода сохраняется в этот же файл если этот результат отличается от содержимого файла, после чего процесс повторяется. И так до стабилизации процесса, т.е. пока данный интерпретатор не будет выдавать тот же текст, который он получил на вход.
Эксперименты показывают, что таким способом неподвижная точки находится не всегда. И это не
удивительно. Теорема о неподвижной точке может быть переформулирована в форме утверждения о том,
что алгоритм преобразования программного кода не может всегда возвращать программу, отличную от
данной. И если неподвижная точка существует, то итерирование применения этого алгоритма может
породить последовательность программ, сходящуюся к неподвижной точке. Но последовательность
может сойтись и к какому-нибудь циклу. Т.е. даже если 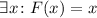 , то возможно
существует последовательность
, то возможно
существует последовательность  такая, что
такая, что 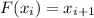 и
и 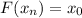 .
Причем, возможно, что
.
Причем, возможно, что 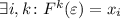 .
.
Обсуждаемый скрипт [33] имеют рудиментарную поддержку определения таких циклов, но для меня остается открытым вопрос о возможности автоматического «преобразования» такого цикла в настоящую неподвижную точку (формально, в цикл из одного элемента).
(Несмотря на наблюдаемую эмпирическую сходимость итераций к неподвижной точке или к циклу, мне
неизвестны какие-либо особые свойства функции 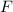 , гарантирующие стабилизацию процесса после
конечного количества шагов.)
, гарантирующие стабилизацию процесса после
конечного количества шагов.)
Другие конструктивные теоремы о неподвижной точке
Пожалуй, это самый спекулятивный и неформальный подраздел этого сообщения. Здесь перечисляются некоторые известные теоремы о неподвижных точках, которые, возможно, могли бы быть применены для конструирования квайнов. Сама эта возможность находится под вопросом, но эти теоремы всё-же заслуживают упоминания в таком контексте.
Первая рекурсивная теорема Клини
(Этот раздел написан по мотивам соответствующего материала из [50].)
Для функций 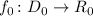 и
и 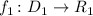 , таких, что
, таких, что 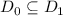 ,
,
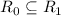 и
и 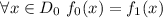 введем обозначение
введем обозначение  ,
читающееся как «
,
читающееся как «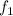 продолжает
продолжает 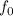 ». (Другими словами, выполняется импликация
». (Другими словами, выполняется импликация
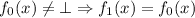 .)
.)
Функция называется конечной если она имеет конечную область определения. Конечной частью
функции 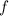 назовём конечную функцию
назовём конечную функцию  . Сопоставим функции
. Сопоставим функции 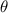 натуральное число
натуральное число 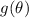 .
.
Подразумевается, что существует алгоритм, который по числам  и
и  вычисляет
вычисляет 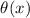 если
существует
если
существует 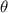 , такая, что
, такая, что 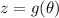 и
и 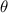 определена в точке
определена в точке  .
.
Оператор 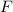 называется рекурсивным оператором если существует вычислимая функция
называется рекурсивным оператором если существует вычислимая функция 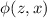 ,
такая, что
,
такая, что 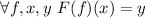 тогда и только тогда, когда существует конечная
тогда и только тогда, когда существует конечная
 , такая, что
, такая, что 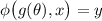 .
.
Оператор 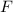 непрерывен если
непрерывен если 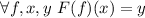 тогда и только тогда, когда существует
конечная
тогда и только тогда, когда существует
конечная  , такая, что
, такая, что 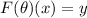 .
.
Оператор 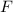 называют монотонным, если
называют монотонным, если 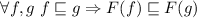 .
.
Утверждение (без доказательства).
Рекурсивные операторы непрерывны и монотонны.
Теорема (без доказательства).
Для любого рекурсивного оператора 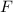 существует неподвижная точка
существует неподвижная точка 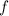 , т.е.
, т.е. 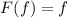 . Причём
. Причём
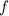 – наименьшая из неподвижных точек, в том смысле, что если для какой-нибудь другой функции
– наименьшая из неподвижных точек, в том смысле, что если для какой-нибудь другой функции
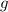 выполняется
выполняется 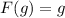 , то
, то  . (Всюду определенная функция
. (Всюду определенная функция 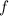 автоматически
будет единственной неподвижной точкой.)
автоматически
будет единственной неподвижной точкой.)
Для демонстрации связи с квайнами в [50] (и это практически единственная обнаруженная мной в
литературе зацепка, связывающая первую рекурсивную теорему с квайнами) по-сути предлагается
попробовать в качестве рекурсивного оператора взять оператор, аналогичный оператору
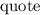 , определенному в разделе о теореме Роджерса (см. выше). Оператор
, определенному в разделе о теореме Роджерса (см. выше). Оператор
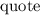 преобразует программу
преобразует программу 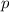 в программу, печатающую текст
в программу, печатающую текст 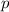 , а по только
что изложенной первой рекурсивной теореме Клини, рекурсивный оператор (с семантикой оператора
, а по только
что изложенной первой рекурсивной теореме Клини, рекурсивный оператор (с семантикой оператора
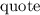 ) должен иметь неподвижную точку
) должен иметь неподвижную точку 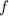 и если из этого следует, что и сам
оператор
и если из этого следует, что и сам
оператор 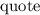 имеет неподвижную точку
имеет неподвижную точку 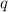 , такую, что
, такую, что 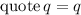 , то, коль скоро программа
, то, коль скоро программа 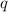 равна программе, печатающей себя,
равна программе, печатающей себя,  есть квайн.
есть квайн.
Здесь уместно прокомментировать согласованность этого вывода с данным выше определением
рекурсивного оператора, ведь 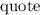 действует не на множестве вычислимых
функций, а на множестве исходных текстов программ. Идея состоит в том, что оператор
действует не на множестве вычислимых
функций, а на множестве исходных текстов программ. Идея состоит в том, что оператор
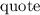 , преобразуя некоторую программу
, преобразуя некоторую программу 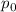 в программу
в программу 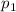 , порождает
рекурсивный оператор
, порождает
рекурсивный оператор 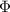 , преобразующий функцию
, преобразующий функцию 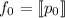 в функцию
в функцию
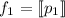 . Обозначим
. Обозначим 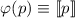 , тогда
вышеописанную идею можно проиллюстрировать следующей диаграммой:
, тогда
вышеописанную идею можно проиллюстрировать следующей диаграммой:
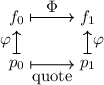
К оператору 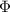 напрямую применима первая рекурсивная теорема, т.е. существует
напрямую применима первая рекурсивная теорема, т.е. существует 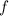 , такая,
что
, такая,
что 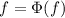 . Из этого следует, что существуют программы
. Из этого следует, что существуют программы 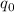 и
и 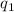 , причем
, причем

Т.к.,
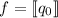 и
и
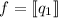 , то
, то 
Подставляя (4) в (5) и применяя определение оператора
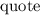 получаем
получаем
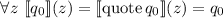 , т.е.
, т.е. 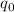 удовлетворяет «уравнению квайна»
удовлетворяет «уравнению квайна» 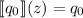 и,
соответственно, является квайном.
и,
соответственно, является квайном.
(Для меня остается открытым вопрос о возможности применения первой рекурсивной теоремы для автоматического конструирования квайнов, как в случае со второй рекурсивной теоремой.)
Теорема Клини о неподвижной точке [из теории решёток]
Произвольное отображение 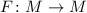 , непрерывное по Скотту и определенное на полном
частично упорядоченном множестве
, непрерывное по Скотту и определенное на полном
частично упорядоченном множестве 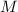 с отношением порядка
с отношением порядка  имеет наименьшую
неподвижную точку.
имеет наименьшую
неподвижную точку.
Непрерывность по Скотту означает существование 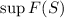 и выполнение
и выполнение 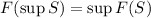 для всякого направленного подмножества
для всякого направленного подмножества 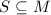 .
.
Теорема Кнастера-Тарского
В [37] приведена теорема о существовании неподвижных точек монотонных отображений на полной
решетке. Пусть 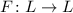 – монотонное отображение на полной решетке
– монотонное отображение на полной решетке 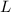 с отношением
частичного порядка
с отношением
частичного порядка  . Т.е.
. Т.е. 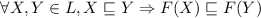 . Теорема Тарского утверждает, что
. Теорема Тарского утверждает, что 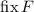 , i.e. множество
неподвижных точек отображения
, i.e. множество
неподвижных точек отображения 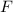 , само является непустой полной решеткой.
, само является непустой полной решеткой.
В [38] доказана конструктивная версия этой теоремы. До этой работы, неподвижные точки монотонных
отображений уже конструировали как 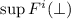 , где
, где 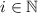 , а
, а 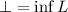 . Но
это требовало от
. Но
это требовало от 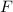 непрерывности по Скотту. В [38] же доказывается теорема, которая не требует
от
непрерывности по Скотту. В [38] же доказывается теорема, которая не требует
от 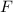 этого свойства и утверждая, что
этого свойства и утверждая, что 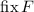 является полной решеткой
относительно
является полной решеткой
относительно  , предлагает, среди прочего, рецепт вычисления неподвижной точки в
виде
, предлагает, среди прочего, рецепт вычисления неподвижной точки в
виде 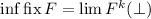 .
.
Здесь 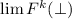 определяется как предел стационарной последовательности
определяется как предел стационарной последовательности
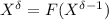 при
при 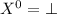 . Считается, что
. Считается, что 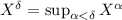 для предельного ординала
для предельного ординала 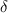 . Под стационарностью понимается, что начиная с
некоторго индекса, элементы последовательности имеют одно и то же значение. Для корректного
погружения в использованные в [38] трансфинитные определения необходимо чтение оригинальной
статьи.
. Под стационарностью понимается, что начиная с
некоторго индекса, элементы последовательности имеют одно и то же значение. Для корректного
погружения в использованные в [38] трансфинитные определения необходимо чтение оригинальной
статьи.
(Эти результаты обобщаются на случай полных частично упорядоченных множеств, только направленные, а не произвольные подмножества которых обязаны иметь супремум.)
Комбинатор неподвижной точки в лямбда-исчислении
В 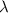 -исчислении [34] для реализации рекурсии используются комбинаторы неподвижной точки,
в основном
-исчислении [34] для реализации рекурсии используются комбинаторы неподвижной точки,
в основном 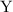 -комбинатор. Этот комбинатор определяется уравнением
-комбинатор. Этот комбинатор определяется уравнением 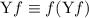 и в соответствии с этим определением вычисляет неподвижную точку функции
и в соответствии с этим определением вычисляет неподвижную точку функции 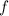 ,
т.е. такое выражение
,
т.е. такое выражение  , что
, что 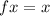 .
.
Если конкретная реализация 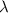 -исчисления поддерживает рекурсивные определения именованных
символов, то вышеприведенного определения достаточно для работы с
-исчисления поддерживает рекурсивные определения именованных
символов, то вышеприведенного определения достаточно для работы с 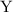 -комбинатором
(могут возразить, что в таком случае он не особо-то и нужен; однако, здесь
-комбинатором
(могут возразить, что в таком случае он не особо-то и нужен; однако, здесь 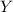 -комбинатор может
служить полезной обёрткой для некоторых функций, позволяющей, к примеру, добавить временное
хранение промежуточных результатов с целью исключения их повторного вычисления, — т.е.,
кэширование, — и, соответственно, получить ускорение в духе динамического программирования).
-комбинатор может
служить полезной обёрткой для некоторых функций, позволяющей, к примеру, добавить временное
хранение промежуточных результатов с целью исключения их повторного вычисления, — т.е.,
кэширование, — и, соответственно, получить ускорение в духе динамического программирования).
В чистом же 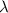 -исчислении требуется определить
-исчислении требуется определить 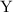 -комбинатор в явном виде,
например как
-комбинатор в явном виде,
например как 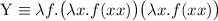 (известный как комбинатор Карри или парадоксальный комбинатор) или, в случае
использования императивного языка, задействовать [энергичный] комбинатор Тьюринга
(известный как комбинатор Карри или парадоксальный комбинатор) или, в случае
использования императивного языка, задействовать [энергичный] комбинатор Тьюринга 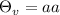 , где
, где 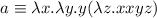 .
.
Теорема о неподвижной точке.
Несмотря на неочевидность этого утверждения, в нетипизированном 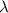 -исчислении любое
выражение имеет неподвижную точку (хотя бы одну).
-исчислении любое
выражение имеет неподвижную точку (хотя бы одну).
Доказательство.
Пусть 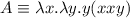 . Комбинатор Тьюринга есть
. Комбинатор Тьюринга есть 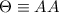 . Утверждается, что для любого
. Утверждается, что для любого 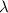 -выражения
-выражения 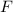 , выражение
, выражение 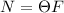 есть
его неподвижная точка. Чтобы увидеть это, запишем следующую цепочку уравнений:
есть
его неподвижная точка. Чтобы увидеть это, запишем следующую цепочку уравнений:
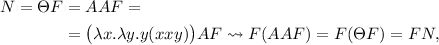
где  обозначает последовательность из нуля или нескольких шагов
обозначает последовательность из нуля или нескольких шагов
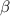 -редукции.
-редукции. 
Теперь 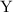 -комбинатор может быть применен для вычисления значений функций, вызывающих
сами себя, в среде, не имеющей возможности выполнять именованный рекурсивный вызов или вообще не
поддерживающей именование объектов.
-комбинатор может быть применен для вычисления значений функций, вызывающих
сами себя, в среде, не имеющей возможности выполнять именованный рекурсивный вызов или вообще не
поддерживающей именование объектов.
Например, если требуется вычислить функцию 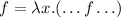 , вызывающую саму себя
по имени
, вызывающую саму себя
по имени 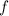 , то можно определить новую функцию
, то можно определить новую функцию 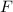 , принимающую
, принимающую 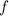 как аргумент:
как аргумент:
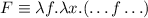 (а при использовании индексов де Брёйна или
бинарного лямбда-исчисления мы можем избавиться и от именованных переменных вовсе). После
определения
(а при использовании индексов де Брёйна или
бинарного лямбда-исчисления мы можем избавиться и от именованных переменных вовсе). После
определения 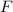 мы можем вычислить
мы можем вычислить 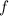 как
как 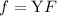 , потому что
, потому что 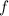 есть неподвижная
точка
есть неподвижная
точка 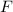 , т.е.,
, т.е.,  , а
, а 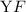 , как было сказано выше,
как раз и находит такую неподвижную точку. Желающие могут непосредственной подстановкой
убедиться, что в этом случае действительно выполняется
, как было сказано выше,
как раз и находит такую неподвижную точку. Желающие могут непосредственной подстановкой
убедиться, что в этом случае действительно выполняется 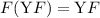 .
.
Учитывая универсальность 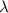 -исчисления и вышеприведенную теорему о неподвижной точке [в
-исчисления и вышеприведенную теорему о неподвижной точке [в
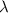 -исчислении], естественно возникает идея об использовании комбинатора неподвижной точки
для конструирования квайнов. (См. также [2, 47].)
-исчислении], естественно возникает идея об использовании комбинатора неподвижной точки
для конструирования квайнов. (См. также [2, 47].)
(Утверждение о существовании комбинатора неподвижной точки практически эквивалентно вышеприведенный первой рекурсивной теореме Клини, но выглядит более конкретным.)
Логическое программирование в ограничениях
В [12, 49] приводится интересный метод генерации квайнов с использованием логического
программирования. Авторы использовали язык логического программирования miniKanren [52],
позволяющий написать на нём аналог «основного уравнения квайнов» 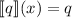 и дать системе решить его относительно
и дать системе решить его относительно 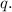
С использованием реализации miniKanren, выполненной на языке scheme, квайны можно
генерировать примерно так (q.scm взят из [49]):
(load "q.scm")
(run 1 (q) (eval-expo q '() q)))
Квайны вычисляются быстро (за секунду) и имеют малые размеры.
(Существует множество реализаций miniKanren и на других языках, e.g., на ECMAScript/JavaScript, Python, Ruby, etc.)
Эволюционные алгоритмы
Крайне интересной представляется потенциальная возможность генерации квайнов с помощью генетических алгоритмов. Среди многих проблем, возникающих при генерации программ эволюционными методами, выделяется проблема сохранения допустимости или синтаксической «корректности» программ при действии генетических операторов (кроссовер, мутация).
В этом смысле, одним из наиболее пригодных представлений для инкрементной эволюционной генерации, являются искусственные нейронные сети (далее ИНС или нейросети). Будучи сетями однотипных нелинейных сумматоров, работа которых зависит от весов связей (синапсов) между ними, нейросети продолжают сохранять работоспособность даже при почти случайных изменениях/«повреждениях» в матрице их весовых коэффициентов. Это довольно сильно контрастирует с традиционными языками программирования, программы на которых с гораздо большей вероятностью подвержены выходу из строя при малейших необдуманных модификациях их исходного текста.
Квайны в виде нейросетей уже известны. В [41] описана ИНС, обучающаяся выводить значения своих же синаптических коэффициентов. Я же хотел бы здесь сосредоточится на другом способе генерации квайнов, а именно на конструировании программ посредством применения генетических алгоритмов к промежуточному представлению на основе нейросетей.
Есть интересный экспериментальный язык Anne, [40], придуманный специально для работы с нейросетями и транслятор neuralbf [16, 51] того же автора, преобразующий программу на bf в описание рекуррентной ИНС. Последняя работа (кому-то могущая показаться несерьёзной) фокусируется на применении генетических алгоритмов для совершенствования и исправления уже написанных вручную программ (вместо их генерации без начального приближения).
Цепные квайны
Назовём цепным квайном (или итеративным квайном) с периодом 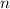 , последовательность
, последовательность 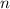 программ
программ
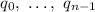 , такую, что
, такую, что 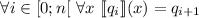 и
и 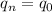 .
.
Можно получить интересное обобщение — многоязыковой или «релейный» квайн — если заменить в
только-что данном определении скобки  на
на 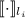 , где
, где 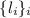 – возможно различные языки программирования
(подразумевается
– возможно различные языки программирования
(подразумевается 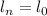 ).
).
Теорема (без доказательства).
Цепные квайны существуют для любого периода 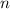 .
.
Всякий, кто пытался писать квайны и цепные квайны, не мог не отметить некоторое отличие в
сложности их написания – цепные квайны [при 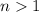 ] обычно проще истинных квайнов (i.e., тоже
цепных квайнов, но с периодом
] обычно проще истинных квайнов (i.e., тоже
цепных квайнов, но с периодом 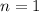 ).
).
Соответственно, не может не возникнуть вопрос о реализуемости полностью автоматического
преобразования данной последовательности 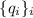 в настоящий квайн
в настоящий квайн 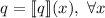 .
.
Генератор квайнов, не зависимый от языка
В разделе о конструировании квайнов на основе второй рекурсивной теоремы Клини, приводился готовый рецепт, алгоритм генерации квайна для конкретного заранее выбранного языка программирования. (Похожий алгоритм возможен и в контексте доказательства теоремы Роджерса.) Возможно, что слово «алгоритм» здесь можно понимать более формально и буквально.
Представляется интересным вопрос о существовании программы 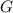 , — «квайнтификатора», —
генерирующей квайн на указанном языке
, — «квайнтификатора», —
генерирующей квайн на указанном языке 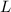 с использованием некоторого количества образцов кода
на этом языке. Причем и разумной спецификацией языка
с использованием некоторого количества образцов кода
на этом языке. Причем и разумной спецификацией языка 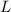 и одновременно образцом кода на нём
может служить интерпретатор языка
и одновременно образцом кода на нём
может служить интерпретатор языка 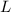 (существующий по теореме об универсальной функции).
(существующий по теореме об универсальной функции).
Чуть более формально задача может быть поставлена так. Пусть дан интерпретатор 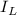 языка
языка 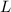 ,
написанный на своем же входном языке, т.е. для любой программы
,
написанный на своем же входном языке, т.е. для любой программы 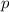 на языка
на языка 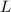 выполняется
выполняется
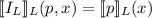 . Пусть также
. Пусть также 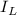 оттранслирован
на референсный язык (семантические скобки без индекса) и существует на нём в виде программы
оттранслирован
на референсный язык (семантические скобки без индекса) и существует на нём в виде программы
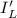 . В этом случае справедливо
. В этом случае справедливо 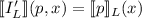 .
.
Спрашивается, как может выглядеть программа 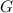 , такая, что
, такая, что 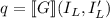 и
и 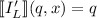 ? Выше мы видели, что
? Выше мы видели, что 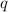 есть неподвижная точка
(по Роджерсу) оператора
есть неподвижная точка
(по Роджерсу) оператора 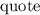 . При попытке реализовать
. При попытке реализовать 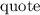 выясняется,
что структура соответствующей программы сильно схожа со структурой интерпретатора. Возможно, это
сходство можно использовать для написания
выясняется,
что структура соответствующей программы сильно схожа со структурой интерпретатора. Возможно, это
сходство можно использовать для написания 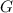 … Но это требует дальнейшего обдумывания.
… Но это требует дальнейшего обдумывания.
Вместо самоинтерпретаторов можно использовать обычно более простые программы, —
специализаторы, — реализующие 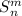 -функцию, ведь именно она является главным ингредиентом
(после диагонализации, конечно) в доказательстве теоремы Клини о рекурсии. (В следующих
сообщениях этот вопрос, возможно, будет исследован более подробно.)
-функцию, ведь именно она является главным ингредиентом
(после диагонализации, конечно) в доказательстве теоремы Клини о рекурсии. (В следующих
сообщениях этот вопрос, возможно, будет исследован более подробно.)
Заключение
Целью этого сообщения была демонстрация возможности автоматического конструирования квайнов на
языке редактора sed с использованием доказательства второй рекурсивной теоремы Клини в качестве
основы. Результат проведенного эксперимента можно считать положительным, хотя автоматическим
такой способ написания квайнов можно назвать только в смысле достаточности запуска единственного
скрипта generate.sh и ликвидации наиболее сложной, и, если можно так выразиться, творческой
составляющей в конструировании самореплицирующейся системы.
В целом, сообщение уже немного вышло за рамки очерченных целей. Но о квайнах можно сказать больше… В следующих сообщениях этой серии.
Ссылки
- [1] http://www.madore.org/~david/computers/quine.html
- [2] http://math.berkeley.edu/~kmill/blog/blog_2018_5_31_universality_quines.html
- [3] http://en.wikipedia.org/wiki/Smn_theorem
- [4] http://en.wikipedia.org/wiki/partial_evaluation
- [5] http://fi.ftmr.info
- [6] http://ru.wikipedia.org/wiki/диагональный_аргумент
- [7] http://ru.wikipedia.org/wiki/теорема_Кантора
- [8] http://ru.wikipedia.org/wiki/проблема_остановки
- [9] http://ru.wikipedia.org/wiki/автомат_фон_Неймана
- [10] http://ru.wikipedia.org/wiki/зонд_фон_Неймана
- [11] Jiazhen Cai, Robert Paige, Program derivation by fixed point computation, 1989
- [12] William E.Byrd, Eric Holk, Daniel P.Friedman, miniKanren, live and untagged: Quine generation via relational interpreters, 2012
- [14] S.C.Kleene, Introduction to Meta-Mathematics, 1952
- [15] http://en.wikipedia.org/wiki/Quine%27s_paradox
- [16] http://www.domob.eu/projects/neuralbf.php
- [17] https://github.com/MakeNowJust/quine/blob/master/quine.sed
- [18] https://github.com/MakeNowJust/quine
- [19] H.Rogers, Theory of Recursive Functions and Effective Computability
- [20] T.A.Hansen, T.Nikolajsen, J.L.Traff, N.D.Jones, Experiments with Implementation of two Theoretical Constructions
- [21] G.Bonfante, M.Kaczmarek, J-Y.Marion, Toward an Abstract Computer Virology
- [22] G.Bonfante, M.Kaczmarek, J-Y.Marion, A Classification of Viruses through Recursion Theorems, 2007
- [23] Julia L. Lawall, Olivier Danvy, Continuation-Based Partial Evaluation
- [24] Anders Bondorf, Improving Binding Times Without Explicit CPS-Conversion
- [25] D.A.Wheeler, Fully Countering Trusting Trust through Diverse Double-Compiling, 2009
- [26] Douglas R.Hofstadter, Goedel, Escher, Bach: an Eternal Golden Braid, 1979
- [27] P.-M. Binder, Theories of almost everything, 2008
- [28] H.G.Rice, Classes of recursively enumerable sets and their decision problems, 1953
- [29] https://en.wikipedia.org/wiki/Rice_theorem
- [30] Gary P.Thompson II, The quine page (self-reproducing code), http://www.nyx.net/~gthompso/quine.htm
- [31] http://www.nyx.net/~gthompso/self_kim.txt
- [32] http://www.latrobe.edu.au/phimvt/joy
- [33] https://gist.github.com/Circiter/7152686
- [34] http://en.wikipedia.org/wiki/lambda_calculus
- [35] Lawrence S.Moss, Recursion Theorems and Self-Replication Via Text Register Machine Programs
- [36] Neil Jones, Computer implementation and application of Kleene’s s-m-n and recursion theorem.
- [37] A.Tarski, A lattice theoretical fixpoint theorem and its applications, 1955
- [38] P.Cousot, R.Cousot, Constructive versions of Tarski’s fixed point theorems, 1979
- [39] J.Case, S.E.Moelius III, Program Self-Reference in Constructive Scott Subdomains, 2009
- [40] http://compann.sourceforge.net
- [41] O.Chang, H.Lipson, Neural Network Quine, 2018
- [42] http://en.wikipedia.org/wiki/quine
- [43] F.William Lawvere, Diagonal arguments and cartesian closed categories, 1969
- [44] Noson S.Yanofsky, A Universal Approach to Self-Referential Paradoxes, Incompleteness and Fixed Points, 2003
- [45] Jean-Yves Marion, From Turing machines to computer viruses, 2012
- [46] https://github.com/Circiter/quine-kleene-generator
- [47] Kleene Second Recursion Theorem: A Functional Pearl // Proc. ACM Program. Lang., Vol 1, 2018
- [48] Дж. фон Нейман, Теория самовоспроизводящихся автоматов, 1971
- [49] https://github.com/webyrd/quines
- [50] В.М.Зюзьков, Теория алгоритмов: Учебное пособие, 2005
- [51] https://gitlab.com/domob/neuralbf
- [52] https://github.com/miniKanren
- [53] http://www.michaelwehar.com/quines
- [54] http://www.keithschwarz.com/kleene
- [55] http://www.nyx.net/~gthompso/quine-1.1.0.tar.gz
- [56] J.C.Owings младший, Diagonalization and the Recursion Theorem, 1973
- [57] E.Alonso, M.Manzano, Diagonalization and Church’s Thesis: Kleene’s Homework, 2005