Решето Эратосфена на sed.
Описывается сценарий для широко известного текстового редактора sed, генерирующий простые числа с помощью решета Эратосфена. На основе данной реализации решета написан скрипт факторизации чисел, а также скрипты, реализующие альтернативные подходы к обнаружению/детектированию анаграмм и к численной симуляции динамической системы из гипотезы Коллатца. В конце сообщения речь идёт о возможных оптимизациях решета Эратосфена, и, в частности, описывается решето Эйлера, тоже реализованное в виде скрипта для sed.
Содержание:
- Введение
- Теоретическая основа просеивания
- Реализация
- Больше эзотерики
- Об оптимизации
- Вычисление некоторых теоретико-числовых функций просеиванием
- Комплектация поставки
- Ссылки
Введение
Иногда в сценариях (скриптах) для поточного редактора sed требуются простые числа. И, учитывая отсутствие в sed нормальной поддержки арифметики, использование решета Эратосфена [1] выглядит удачным решением для генерации простых чисел прямо в sed-скрипте. Поверхностный поиск в поисковых машинах интернета не дал конкретных результатов, поэтому я решил написать этот скрипт самостоятельно, а в этой заметке рассказать о его работе.
Скрипт (sieve.sed) получился довольно компактным, по крайней мере в том смысле, что код печати
результатов занимает лишь немного меньше половины всего исходного текста. Интересно, что на
основе этой реализации решета не составляет труда написать утилиту факторизации чисел (см.
factor.sed). Фактически, первая версия factor.sed была получена удалением кода печати
результатов (i.e. удалением почти половины кода, см. выше) и добавлением всего одной
строчки/инструкции в код решета. Она печатала факторы в унарной системе счисления и не
определяла степени найденных простых делителей (т.е., строго говоря, находила не все делители).
Её улучшение потребовало некоторых усилий и привело к некоторому увеличению и дублированию кода
(другими словами, существует потенциал для сокращения объема кода factor.sed).
(Обсуждаемые скрипты могут быть найдены в [2].)
Теоретическая основа просеивания
Работа решета заключается в итеративном удалении — вычеркивании — составных чисел из
текущего рабочего множества чисел  . На каждом шаге
. На каждом шаге  удаляются все
числа, кратные очередному найденному простому числу
удаляются все
числа, кратные очередному найденному простому числу 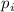 . Новым простым числом
. Новым простым числом 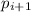 становится наименьшее невычеркнутое число, большее
становится наименьшее невычеркнутое число, большее 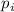 :
: 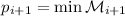 , где
, где
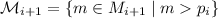 . Если же
. Если же 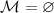 , то процесс
завершается, а последнее множество
, то процесс
завершается, а последнее множество 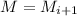 (N.B., равное
(N.B., равное 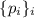 ) становится результатом
его работы.
) становится результатом
его работы.
В качестве начального приближения выбирается интервал 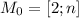 для данного
для данного 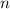 , — длины
решета, — и полагается
, — длины
решета, — и полагается 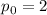 .
.
Более структурированно:
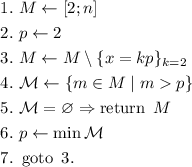
Утверждается, что 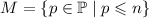 , где
, где 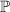 – множество
простых чисел.
– множество
простых чисел.
Набросок доказательства
Озвученный алгоритм порождает индуктивное доказательство.
База: 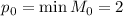 .
.
Предположение индукции: 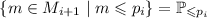 , где
, где
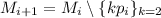 . Эта рекуррентная формула своим следствием имеет
. Эта рекуррентная формула своим следствием имеет
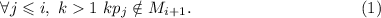
Шаг индукции: необходимо показать, что 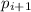 – следующее простое число. Итак, допустим мы
выбрали
– следующее простое число. Итак, допустим мы
выбрали 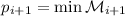 . Факторизуем его,
. Факторизуем его, 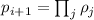 , где
, где
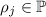 . Формула (1) говорит, что числа, кратные простым
. Формула (1) говорит, что числа, кратные простым 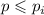 уже
удалены из
уже
удалены из 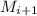 , а значит и из
, а значит и из 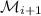 ; поэтому
; поэтому 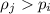 .
.
(Имеется в виду, что для некоторого 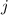 ,
, 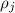 можно вынести за знак произведения:
можно вынести за знак произведения:
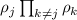 , и именно поэтому
, и именно поэтому 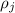 не может быть меньше или равен
не может быть меньше или равен 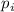 –
такие кратные уже вычеркнуты; если же
–
такие кратные уже вычеркнуты; если же 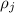 есть единственный множитель, то тем более он
должен быть больше
есть единственный множитель, то тем более он
должен быть больше 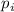 – по определению множества
– по определению множества 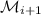 , по которому и берется
минимум для нахождения разлагаемого
, по которому и берется
минимум для нахождения разлагаемого 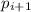 .)
.)
Также понятно, что множители 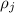 не превышают самого числа
не превышают самого числа 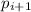 , т.е.
, т.е. 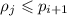 .
.
Конкретно, из 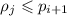 и нефакторизуемости
и нефакторизуемости 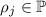 следует, что
следует, что
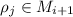 (i.e.,
(i.e., 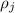 никогда не вычеркивалось и не будет вычеркиваться). А из
никогда не вычеркивалось и не будет вычеркиваться). А из
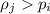 следует, что
следует, что 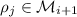 . При этом, если
. При этом, если 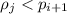 (а не
(а не
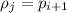 ), то это противоречит минимальности
), то это противоречит минимальности 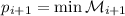 .
.
Значит, от противного, 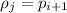 . Т.е.
. Т.е. 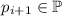 и других простых между
и других простых между
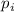 и
и 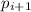 нет (иначе они не были бы вычеркнуты на предыдущих шагах и входили бы в
нет (иначе они не были бы вычеркнуты на предыдущих шагах и входили бы в
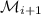 , что опять противоречило бы минимальности
, что опять противоречило бы минимальности 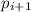 в
в 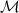 ).
).

Реализация
Принцип работы sieve.sed
Общий пошаговый вид алгоритма:
- Чтение длины решета (конвертация десятичного числа в унарное).
- Просеивание бинарной строки, полученной на основе унарного числа из предыдущего шага.
- Поиск следующего простого, т.е. первой ближайшей единицы, лежащей правее текущего простого.
- Вычеркивание чисел, кратных найденному простому; под вычеркиванием понимается изменение 1 на 0 в соответствующих позициях решета.
- Печать решета.
- Решето проходится слева-направо.
- На каждом шаге инкрементируется счетчик (изначально обнулённый).
- Если в текущей позиции решета записана единица, то значание счётчика выводится на экран.
Возможно есть смысл немного детализировать работу решета на этапе поиска следующего простого
числа. Сначала перед решетом приписывается маркер #. Далее, в уже частично заполненном решете
отыскивается первая единица, лежащая правее маркера #, после чего этот маркер перемещается на
позицию сразу после этой единицы. Длина части решета, лежащей левее маркера есть новое простое
число. Этот префикс копируется на следующую строчку и может считаться записью найденного
простого числа в унарной системе счисления.
После символа # добавляется вспомогательный маркер @, а в начало следующей строки – маркер
:, после чего оба маркера начинают сдвигаться вправо на один символ за раз. Если маркер :
оказывается в конце второй строки, а @ ещё не дошёл до конца первой, то маркер @ с
необходимостью оказывается сразу после следующего составного числа и мы можем записать в эту
позицию ноль, независимо от значения, которое было там ранее. Теперь маркер : возвращается в
начало второй строки.
Процесс перемещения маркеров @ и : продолжается до вычеркивания всех множителей текущего
простого числа (i.e., пока @ не дойдёт до конца первой строки), после чего эти маркеры
удаляются и описанный процесс повторяется.
Принцип работы factor.sed
Этот скрипт написан на основе вышеописанного sieve.sed, но код обнаружения нового
простого числа слегка модифицирован, а после него добавлен код определения показателя степени
для найденного простого множителя.
Число, подлежащее факторизации используется просто в качестве длины решета. Понятно, что простые, входящие в этого решето (и только они) будут входить в разложение данного числа на простые множители.
Поиск следующего простого отличается от аналогичного кода в скрипте sieve.sed фактически лишь
тем, что при обнаружении простого числа обнуляется отдельный счетчик, а при вычеркивании каждого
составного числа этот счётчик инкрементируется. Очевидно, что после вычеркивания всех множителей
текущего простого числа (не выходящих за пределы решета, естественно) значение счётчика будет
равно целой части результата деления исходного факторизуемого числа на текущий простой
множитель.
Далее мы должны просто продолжать делить значение этого счётчика на текущее простое число, пока счётчик не обнулится. Причём после каждой операции деления мы снова переходим к коду, выполненному после обнаружения текущего простого числа (т.е. мы печатаем тоже самое простое число ещё раз, делим счётчик на это простое и т.д.).
В результате, скрипт печатает текущий простой множитель нужное количество раз, а после печати всех простых множителей, мы получаем полное разложение исходного числа, равного длине решета.
Больше эзотерики
Также были написаны два демонстрационных скрипта, anagram.sed и collatz.sed, использующих
простые числа и факторизацию для решения задач, в которых в явном виде простые числа обычно не
применяют. Первый скрипт (вместо которого, естественно, гораздо эффективнее было бы использовать
композицию сортировки символов в строках и сравнения результирующих строк-последовательностей)
реализует идею из [3,4] и эксплуатирует основную теорему
арифметики [5] для детектирования анаграмм, т.е. для определения, являются ли
две данные строки-последовательности перестановками друг-друга. Каждому символу
последовательностей сопоставляется единственным образом некоторое простое число, после чего все
эти числа, соответствующие символам из конкретной строки, перемножаются. Основная теорема
арифметики вместе с коммутативностью умножения гарантируют, что анаграммы будут давать
одинаковые произведения-сигнатуры.
Ранее написанный алгоритм просеивания был модифицирован/упрощён для работы только с двоичными числами. Для умножения двоичных чисел я использовал код из gist’а [6].
Второй скрипт, collatz.sed, реализует известную динамическую систему из гипотезы 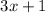 (см.
[7,8]), но вместо привычных операций
(см.
[7,8]), но вместо привычных операций 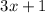 и
и 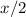 используются
манипуляции с простыми числами, на мой взгляд лучше показывающие истинную теоретико-числовую
суть гипотезы Коллатца.
используются
манипуляции с простыми числами, на мой взгляд лучше показывающие истинную теоретико-числовую
суть гипотезы Коллатца.
Пусть дана функция
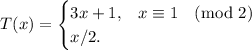
Гипотеза Коллатца утверждает, что 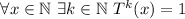 .
Более точно, похоже, что для всех натуральных
.
Более точно, похоже, что для всех натуральных  итерации
итерации 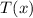 сходятся к циклу
сходятся к циклу 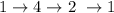 .
.
Если при каждом применении 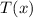 сначала производить разложение
сначала производить разложение  на простые множители, то
деление на два будет сводится к вычеркиванию двойки (на деле, можно заодно вычеркивать все
двойки сразу) из факторизации. Операция
на простые множители, то
деление на два будет сводится к вычеркиванию двойки (на деле, можно заодно вычеркивать все
двойки сразу) из факторизации. Операция 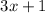 будет соответствовать приписыванию тройки,
перемножению оставшихся факторов и прибавлению единицы к результату.
будет соответствовать приписыванию тройки,
перемножению оставшихся факторов и прибавлению единицы к результату.
Прибавление единицы гарантирует, что результат не будет делиться на всё, на что делилось число
 , или, другими словами, в факторизации результата операции
, или, другими словами, в факторизации результата операции 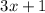 будут задействованы совсем
другие множители, ни одного из которых не было в факторизации
будут задействованы совсем
другие множители, ни одного из которых не было в факторизации  ; с использованием наибольшего
общего делителя,
; с использованием наибольшего
общего делителя, 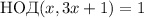 . Добавление же тройки гарантирует, что в
разложении
. Добавление же тройки гарантирует, что в
разложении 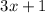 никаких троек тоже не будет, даже если их и не было в разложении
никаких троек тоже не будет, даже если их и не было в разложении  изначально.
изначально.
Если достаточно разнообразных множителей для формирования 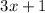 не найдется, это будет
означать, что после вычеркивания двоек у нас останется пустая факторизация, т.е. результат
превратится в единицу.
не найдется, это будет
означать, что после вычеркивания двоек у нас останется пустая факторизация, т.е. результат
превратится в единицу.
(Фактически, мы имеем дело с гонкой двух процессов – процессом «генерации» простых чисел,
скажем, решетом, и процессом их «потребления» за счёт прибавления единицы; судя по
экспериментам, процесс потребления работает быстрее – в какой-то момент, независимо от
стартового значения, новых простых не оказывается в наличии и итерации сходятся к уже
упоминавшемуся циклу 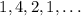 )
)
Гипотеза 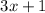 по праву относится к классу задач, многими называемыми «математическими
болезнями»; в таких задачах сочетается предельная простота формулировки условия с неподдающейся
многим математикам сложностью решения, а в данном случае, по всей видимости, вообще с полной
неготовностью современной математики к доказательству этой гипотезы.
по праву относится к классу задач, многими называемыми «математическими
болезнями»; в таких задачах сочетается предельная простота формулировки условия с неподдающейся
многим математикам сложностью решения, а в данном случае, по всей видимости, вообще с полной
неготовностью современной математики к доказательству этой гипотезы.
Об оптимизации
В этом сообщении и в предложенных скриптах вообще не применяются распространённые оптимизации
решета Эратосфена. Но для полноты картины, наверное стоит упомянуть возможные направления для
улучшения. Во-первых, можно ограничиться рассмотрением только чисел 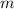 , таких, что
, таких, что 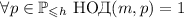 для некоторого
для некоторого 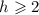 ;
e.g., при
;
e.g., при 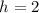 это соответствует игнорированию всех чётных чисел, больших двух, всегда
по-определению являющихся составными.
это соответствует игнорированию всех чётных чисел, больших двух, всегда
по-определению являющихся составными.
Во-вторых, перебор кратных для нечётных простых чисел 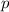 можно вести с шагом
можно вести с шагом 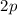 , а не
, а не 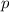 ;
при использовании вышеописанного обобщения на случай чисел
;
при использовании вышеописанного обобщения на случай чисел 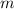 , взаимно простых с несколькими
первыми простыми числами [не превышающими
, взаимно простых с несколькими
первыми простыми числами [не превышающими 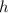 ], можно генерировать кратные так, чтобы они
тоже были взаимно простыми с числами из
], можно генерировать кратные так, чтобы они
тоже были взаимно простыми с числами из 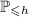 . См. также [9].
. См. также [9].
В-третьих, процесс вычеркивания чисел, кратных очередному найденному простому 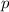 , можно
начинать сразу с
, можно
начинать сразу с 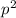 , а не с
, а не с 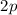 ; как следствие, не имеет смысла продолжать вычеркивание
кратных если
; как следствие, не имеет смысла продолжать вычеркивание
кратных если 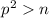 . Т.е., множители для
. Т.е., множители для 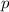 , использующиеся при вычеркивании составных чисел,
образуют множество
, использующиеся при вычеркивании составных чисел,
образуют множество 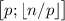 (максимум здесь выбран так, чтобы после
умножения на
(максимум здесь выбран так, чтобы после
умножения на 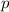 получилось
получилось 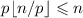 , а минимум соответствует началу
вычеркивания с
, а минимум соответствует началу
вычеркивания с 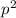 ).
).
(Естественно, желающие могут попробовать добавить эти оптимизации в обсуждаемый скрипт, хотя с квадратами в sed, наверное, лучше не связываться).
Решето Эйлера
Решето Эратосфена может вычеркивать одни и те же числа по нескольку раз. Эйлер придумал (для
решаемой им в тот момент вполне практической математической задачи) модификацию [10] решета, позволяющую вычеркивать составные числа только один раз. Алгоритм можно
описать так:
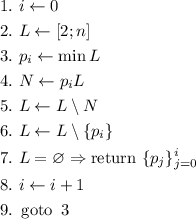
Здесь 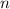 является длиной решета (как и в ранее описанном алгоритме для решета Эратосфена).
Сгенерированные простые числа коллекционируются в множестве
является длиной решета (как и в ранее описанном алгоритме для решета Эратосфена).
Сгенерированные простые числа коллекционируются в множестве 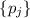 , которое и возвращается
при завершении работы алгоритма.
, которое и возвращается
при завершении работы алгоритма.
Все операции производятся с рабочим множеством чисел 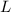 , изначально равным отрезку
, изначально равным отрезку 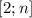 . На
каждой итерации выбирается минимальный элемент
. На
каждой итерации выбирается минимальный элемент 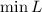 этого множества и объявляется следующим
простым числом (сразу же сохраняемым в
этого множества и объявляется следующим
простым числом (сразу же сохраняемым в 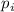 при текущем значении
при текущем значении  ), после чего формируется
новое множество произведений
), после чего формируется
новое множество произведений 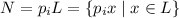 , т.е., числа кратные
, т.е., числа кратные 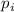 , но ещё не
ни разу не вычеркнутые, помечаются для последующего удаления. После этого, помеченные числа
удаляются из рабочего множества с помощью теоретико-множественной операции вычитания
, но ещё не
ни разу не вычеркнутые, помечаются для последующего удаления. После этого, помеченные числа
удаляются из рабочего множества с помощью теоретико-множественной операции вычитания 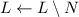 . Ставший теперь ненужным элемент
. Ставший теперь ненужным элемент 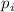 , до сих пор остававшийся в множестве
, до сих пор остававшийся в множестве 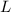 (т.к. до этого, при формировании вспомогательного множества помеченных чисел
(т.к. до этого, при формировании вспомогательного множества помеченных чисел 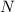 , умножался как
минимум на 2), удаляется из
, умножался как
минимум на 2), удаляется из 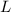 . И если это множество стало пустым, то алгоритм завершается, в
противном же случае инкрементируется счётчик итераций
. И если это множество стало пустым, то алгоритм завершается, в
противном же случае инкрементируется счётчик итераций  и процесс повторяется (с поиска нового
минимального элемента
и процесс повторяется (с поиска нового
минимального элемента 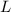 ).
).
Несмотря на некоторые внешние различия, суть этого алгоритма всё та же: для каждого очередного простого числа из решета удаляются/вычеркиваются все числа, кратные ему, в результате чего следующее невычеркнутое число тоже оказывается простым. Итерирование этих манипуляций приводит к «просеиванию» исходного набора чисел и к удалению всех составных чисел (в решете Эйлера, в отличии от оригинального решета Эратосфена, простые числа тоже удаляются из рабочего множества, но по мере их обнаружения они накапливаются в другом множестве или, скажем, выводятся на печать).
Важно, что элементы, помечаемые для удаления (т.е. добавляемые в 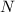 ), по прежнему участвуют в
процессе пополнения множества
), по прежнему участвуют в
процессе пополнения множества 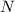 .
.
(Нижеследующий материал написан по мотивам [11].)
Чем же обеспечивается главное свойство решета Эйлера, т.е. почему в 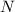 никогда не попадают уже
удаленные из
никогда не попадают уже
удаленные из 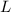 числа? Если в
числа? Если в 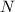 попало число, большее
попало число, большее 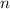 , то оно, очевидно, не может быть
удалено повторно из
, то оно, очевидно, не может быть
удалено повторно из 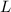 , так как там таких больших чисел просто не было изначально:
, так как там таких больших чисел просто не было изначально: 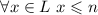 по построению. Если же
по построению. Если же 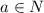 не превышает
не превышает 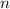 , то исходя из смысла
присваивания
, то исходя из смысла
присваивания 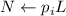 (см. шаг 4 вышеприведенного алгоритма),
(см. шаг 4 вышеприведенного алгоритма), 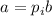 , где
, где 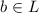 .
.
Суть в том, что любое натуральное число  можно единственным образом представить в виде
можно единственным образом представить в виде
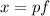 , где
, где 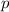 – наименьший простой делитель (фактор) числа
– наименьший простой делитель (фактор) числа  . При этом среди факторов числа
. При этом среди факторов числа
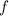 , очевидно, не будет чисел, меньших
, очевидно, не будет чисел, меньших 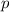 . (Т.е. мы просто «отсоединяем» наименьший фактор
. (Т.е. мы просто «отсоединяем» наименьший фактор
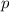 от
от  и формируем разложение
и формируем разложение 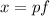 полагая
полагая 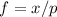 ; тогда из основной теоремы арифметики
[5], т.е. из единственности факторизации, как раз и следует единственность
требуемого разложения
; тогда из основной теоремы арифметики
[5], т.е. из единственности факторизации, как раз и следует единственность
требуемого разложения 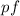 .)
.)
Применительно к решету, это означает, что для текущего найденного простого 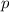 , множество
, множество
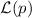 множителей, при перемножении
множителей, при перемножении 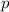 на которые будут получаться новые составные
числа, подлежащие вычеркиванию, равно
на которые будут получаться новые составные
числа, подлежащие вычеркиванию, равно 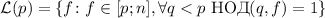 .
.
Покажем, что такое определение 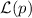 совпадает с
совпадает с 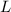 из алгоритма (см. выше). На
каждой итерации, если
из алгоритма (см. выше). На
каждой итерации, если 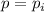 , то
, то 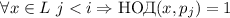 , т.е. все числа из
, т.е. все числа из 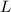 , большие чем
, большие чем 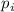 не делятся на простые меньшие
не делятся на простые меньшие 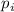 ведь
составные числа, делящиеся на
ведь
составные числа, делящиеся на 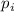 уже были вычеркнуты на предыдущих итерациях алгоритма.
(Здесь идет речь об
уже были вычеркнуты на предыдущих итерациях алгоритма.
(Здесь идет речь об 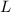 до шага 5, т.е. до операции
до шага 5, т.е. до операции 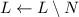 .)
.)
Т.о., 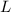 содержит числа из промежутка
содержит числа из промежутка 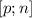 , не делящиеся на простые, меньшие
, не делящиеся на простые, меньшие 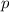 , т.е.
, т.е.
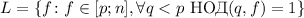 . Это совпадает с
выражением для
. Это совпадает с
выражением для 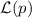 .
.
Осталось показать, что 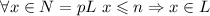 , т.е., что подлежащие
вычеркиванию числа
, т.е., что подлежащие
вычеркиванию числа 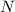 уже присутствуют в
уже присутствуют в 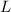 (либо просто выходят за пределы решета) и их не
придётся вычеркивать повторно. Как мы уже выяснили, каждый такой
(либо просто выходят за пределы решета) и их не
придётся вычеркивать повторно. Как мы уже выяснили, каждый такой 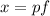 , для некоторого
, для некоторого 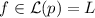 единственен и так как на всех предыдущих итерациях алгоритма мы удаляли лишь
числа, наименьший фактор которых был меньше
единственен и так как на всех предыдущих итерациях алгоритма мы удаляли лишь
числа, наименьший фактор которых был меньше 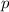 , то из
, то из 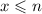 и начального приближения
для
и начального приближения
для 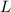 , равного
, равного 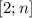 , как раз и следует, что
, как раз и следует, что 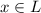 .
.
За более подробной информацией о решете Эйлера следует обратиться, e.g., к [1,12,11] . Интересно, что в некоторых работах, например, в той же [12], прямые отсылы к Эйлеру отсутствуют, поэтому иногда говорят, что это решето неоднократно переизобреталось различными авторами.
Возможно, что причиной этого библиографического казуса является некоторая неявность введения
решета в работе Эйлера. Эйлер игрался с 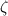 -функцией Римана, разлагающейся в ряд Дирихле
-функцией Римана, разлагающейся в ряд Дирихле

для
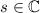 . Для доказательства важного
тождества
. Для доказательства важного
тождества 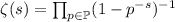 , Эйлер строил последовательность
, Эйлер строил последовательность
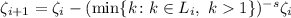 начиная с
начиная с 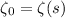 .
Здесь
.
Здесь  – такое множество, что
– такое множество, что 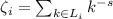 .
.
Сначала, естественно, 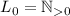 , и поэтому
, и поэтому 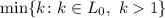 равен 2,
т.е. первому простому числу. Умножение
равен 2,
т.е. первому простому числу. Умножение 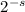 на сумму
на сумму 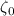 , равную
, равную 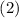 даёт новую
сумму, в которой все основания кратны двум. Соответственно, вычитание
даёт новую
сумму, в которой все основания кратны двум. Соответственно, вычитание 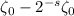 обнулит в
обнулит в 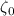 такие слагаемые (в данном случае, с чётными основаниями степеней). Если
построить для только что полученной суммы
такие слагаемые (в данном случае, с чётными основаниями степеней). Если
построить для только что полученной суммы 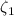 множество оснований
множество оснований 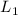 , то окажется, что
, то окажется, что
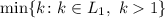 равно трём – второму простому числу. Продолжая этот процесс мы
будем на каждом шаге получать новое простое число и использовать его для обнуления/вычеркивания
слагаемых с основаниями, кратными ему, фактически, воспроизводя просеивание Эратосфена/Эйлера
без повторных вычеркиваний. (Кстати, нетрудно видеть, что здесь множество
равно трём – второму простому числу. Продолжая этот процесс мы
будем на каждом шаге получать новое простое число и использовать его для обнуления/вычеркивания
слагаемых с основаниями, кратными ему, фактически, воспроизводя просеивание Эратосфена/Эйлера
без повторных вычеркиваний. (Кстати, нетрудно видеть, что здесь множество 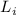 почти полностью
соответствует множеству
почти полностью
соответствует множеству 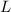 из разобранного ранее алгоритма решета Эйлера; разве что в
из разобранного ранее алгоритма решета Эйлера; разве что в 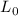 есть лишняя единица…)
есть лишняя единица…)
Даёт ли решето Эйлера ускорение?
При работе решета Эратосфена требуется вычеркнуть числа, кратные всем простым 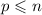 .
Для каждого
.
Для каждого 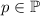 , очевидно, требуется
, очевидно, требуется 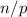 вычеркиваний. Т.о. для оценки количества
требуемых операций нужно просуммировать это выражение по всем простым, не превышающим
вычеркиваний. Т.о. для оценки количества
требуемых операций нужно просуммировать это выражение по всем простым, не превышающим 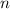 , т.е.
общее количество операций равно
, т.е.
общее количество операций равно 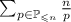 . Известно, что
. Известно, что
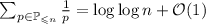 . Таким образом,
временна́я асимптотическая сложность решета Эратосфена оценивается как
. Таким образом,
временна́я асимптотическая сложность решета Эратосфена оценивается как
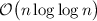 , где
, где 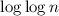 выполняет роль среднего количества
различных делителей числа
выполняет роль среднего количества
различных делителей числа 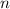 . (N.B., за
. (N.B., за  -нотацией ещё прячется слагаемое
-нотацией ещё прячется слагаемое
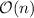 , т.е. время, требуемое на инициализацию решета построением множества
, т.е. время, требуемое на инициализацию решета построением множества 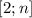 .)
.)
Эта асимптотическая оценка становится линейной (если вычеркивание очередного числа выполняется
за константное 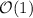 время) в случае решета Эйлера. Для языка программирования с
дешёвым умножением это позволяет работать решету Эйлера быстрее (в теории):
время) в случае решета Эйлера. Для языка программирования с
дешёвым умножением это позволяет работать решету Эйлера быстрее (в теории): 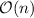 против
против 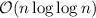 .
.
Но sed, очевидно, не относится к таким языкам – в нём вообще нет понятия умножения, хотя универсальность sed и позволяет реализовать умножение низкоуровневыми средствами. Причем, выбранный для рассматриваемой здесь реализации решета Эйлера способ умножения в унарной системе счисления, полностью нивелирует какие бы то ни было преимущества этого варианта решета.
Фактически, поличившийся код работает даже медленнее чем исходное решето Эратосфена или его
наивная «эйлерофикация» заменой s/1@/0@/ на /1@/ s/1@/0@/. :) Но раз он всё-таки был
написан, то я включил файл euler-sieve.sed в основной репозиторий [2].
Решето Эйлера могло бы быть полезным в гипотетическом случае просеивания чисел, находящихся не в оперативной памяти, а на носителе типа flash-микросхем, имеющем ограничение на количество операций перезаписи содержимого. Кроме этого, можно вообразить ситуацию с просеиванием чисел в удалённой базе данных: в этом случае решето Эйлера позволяет минимизировать как восходящий (для отправки команд записи/вычеркивания), так и нисходящий (для считывания содержимого ячеек решета) сетевой трафик. Наконец, при теоретико-игровой интерпретации, это решето сгодилось бы при [даже ещё более гипотетической] игре типа «морской бой», в которой состояние поля-решета замаскировано «туманом войны» и можно получать лишь прореженные сведения о последнем найденном простом числе. При этом нельзя попадать в «своих» (в простые числа) или тратить «боеприпасы» и время впустую в попытках вычеркивания уже вычеркнутых чисел.
Похоже, что у решета Эйлера в реальности два применения – ускорение генерации простых чисел при использовании подходящих языков программирования типа C, и применение теоретическое (для чего, собственно, Эйлер и придумал это решето [10]), e.g. в задачах, требующих единственности каждого генерируемого решетом составного числа.
Принцип работы euler-sieve.sed
Скрипт euler-sieve.sed получен из sieve.sed исправлением нескольких строчек. Набор
вспомогательных маркеров был расширен с #@: до #_@:,. Маркет # как и прежде находится
после очередного найденного простого числа. Справа от него находится маркер _, отмечающий
очередной множитель, на который требуется умножить текущее простое число (N.B., если _ стоит
сразу после #, то это означает, что множителем будет само простое число, т.е. это
соответствует вычислению 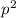 ). Маркер движется вправо и устанавливается на следующее
невычеркнутое число.
). Маркер движется вправо и устанавливается на следующее
невычеркнутое число.
Для каждого положения маркеров # и _, префиксы, состоящие из символов, расположенных левее
каждого из этих маркеров, копируются на две следующие за решетом строки. Из префиксов удаляются
лишние символы (в т.ч. вышеупомянутые маркеры), а перед префиксами добавляются новые маркеры:
маркер : перед первым префиксом и , – перед вторым. Оба префикса, т.о., всего-лишь
обозначают подлежащие перемножению числа [в унарной системе счисления]. Их произведение следует
вычеркнуть из решета.
Для этого перед решетом добавляется маркер @ (N.B., изначально левее маркеров # и _, что
контрастирует с вышеописанным кодом для решета Эратосфена). Далее, в двух вложенных циклах
начинают смещаться вправо маркеры : и ,. Причем маркер , смещается на одну позицию когда
маркер : доходит до конца его строки. После каждого смещения маркера , маркер :
реинициализируется и вновь оказывается перед своей строкой. При каждом перемещении маркера :
на одну позицию, на одну позицию вправо смещается и маркер @. Т.к. на пути маркера @ лежат
маркеры # и _ (которых он гарантированно обгонит), то после окончания работы обоих циклов,
т.е. по достижению маркером , конца своей строки, позиция @ корректируется, смещаясь вправо
на две позиции.
В конечном счета, маркер @ оказывается сразу после составного числа, равного произведению двух
выделенных префиксов и подлежащего вычеркиванию. Однако, если в реализации решета Эратосфена, на
аналогичном этапе производилось, собственно, вычеркивание командой s/1@/0@/, то сейчас
выбранный элемент решета лишь помечается к удалению, заменяясь не на 0, а на x.
После всего этого мы можем перейти к новой итерации по перемещению маркера _, отмечающего
следующий множитель для текущего простого числа (маркер _ перепрыгивает к первому ненулевому
символу, лежащему правее него). Если же правее маркера _ не оказалось ни одного символа 1
или x (т.е. невычеркнутого, хотя, возможно, и помеченного числа), то все помеченные к удалению
числа вычеркиваются окончательно командой s/x/0/g и мы переходим к следующей итерации смещения
маркера #. Если правее от маркера # не оказывается простых чисел, т.е. если нет ячеек со
значением 1, то алгоритм просеивания завершает свою работу, передавая управление финальной
части скрипта, производящей печать результатов.
Вычисление некоторых теоретико-числовых функций просеиванием
(Этот раздел был добавлен в апреле 2021 г.)
[Модифицированное] решето Эратосфена может применяться для вычисления некоторых функций, хорошо известных в теории чисел. Примеры таких функций [13]:
- Простота числа; основное применение обычного решета Эратосфена.
- Радикал целого числа (функция
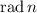 );
); 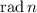 равен
произведению всех различных простых делителей числа
равен
произведению всех различных простых делителей числа 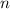 .
.
- Функция Эйлера (
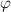 -функция);
-функция); 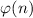 равно количеству чисел, взаимно простых с
равно количеству чисел, взаимно простых с
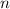 .
.
- Количество различных простых делителей (
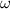 -функция).
-функция).
- Наименьший простой делитель.
- Факторизация (разложение на простые множители).
Комплектация поставки
-
plain-sieve.sed– принимает длину решета и возвращает бинарную последовательность с единицами только в позициях, соответствующих простым числам (самая первая, левая позиция соответствует единице и поэтому всегда равна 0).Пример:
echo 10 | ./plain-sieve.sedвернёт0110101000(единицы в позициях 2, 3, 5 и 7). -
sieve.sed– основной скрипт (кратко описанный в разделе «Реализация»; см. выше), принимающий длину решета и возвращающий (точнее говоря, печатающий) список (с разделением переводом строки) простых чисел, не превышающих данной длины.Пример:
echo 10 | ./sieve.sedвозвращает:2 3 5 7 -
binary-sieve.sed– скрипт аналогичен предыдущему, но работает в двоичной системе счисления (i.e. и длину решета принимает в виде бинарного числа и простые числа печатает тоже в двоичной записи; это немного упрощает код чтения и печати чисел) .Пример:
echo 1010 | ./binary-sieve.sed 10 11 101 111Действительно,
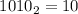 ,
, 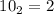 ,
, 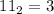 ,
, 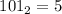 и
и 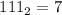 .
. -
anagram.sedиcollatz.sedбыли описаны в предыдущем разделе этого сообщения. Скриптanagram.sedсейчас поддерживает только латинские символы, аcollatz.sedпечатает только «ключевые» точки траектории , т.е. строит последовательность итерируя отображение
, т.е. строит последовательность итерируя отображение
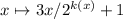 , где
, где 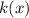 есть [максимальная] степень множителя 2 в факторизации
числа
есть [максимальная] степень множителя 2 в факторизации
числа  . E.g. для начального числа
. E.g. для начального числа 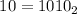 будет построена последовательность
будет построена последовательность 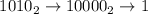 , i.e. 10 будет поделено на 2, затем этот результат без печати на экране будет
утроен и инкрементирован, что даст 16 (
, i.e. 10 будет поделено на 2, затем этот результат без печати на экране будет
утроен и инкрементирован, что даст 16 (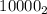 ), а это последнее число будет напечатано и
сразу же [целочисленно] разделено на максимально возможную здесь степень двойки,
), а это последнее число будет напечатано и
сразу же [целочисленно] разделено на максимально возможную здесь степень двойки, 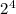 , что
даст последнюю точку траектории, 1.
, что
даст последнюю точку траектории, 1. -
anagrams.txt– примеры анаграмм для тестированияanagram.sed. -
factor.sed– производит разложение данного числа на простые множители (работа скрипта уже была описана в резделе «Реализация»).Пример:
echo 18 | ./factor.sed 2 3 3Как и ожидалось,
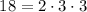 .
. -
factor-hack-unary.sed– простой скрипт, вместо решета использующий «обратные ссылки» в регулярном выражении (следуя [14,15,16]) для факторизации числа, представленного в унарной системе счисления.Примечание: здесь используются расширенные «регулярные» выражения, поддерживающие ссылки вида
\1,\2, etc., и не являющиеся именно регулярными в привычном смысле – такие выражения с обратными ссылками не удастся скомпилировать в конечный автомат.Скрипт на самом деле имеет дело со списком чисел (разделенных переводом строки), подлежащих разложению. Но разложению подвергается только одно из них, помеченное специальным маркером.
Для числа
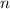 используется регулярное выражение, аналогичное выражению
используется регулярное выражение, аналогичное выражению /^(11+)(\1+)$/. Как видно, оно выделяет некую группу из не менее чем двух единиц при помощи подвыражения(11+), т.е. выделяет один множитель (возможно составной),
и с помощью подвыражения
(возможно составной),
и с помощью подвыражения (\1+)проверяет, можно ли представить оставшуюся часть числа конкатенацией некоторого ненулевого количества копий этой группы (без остатка).Если это не удалось сделать, то
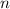 либо равно единице, либо является простым. В противном
случае скрипт производит деление числа на найденный множитель:
либо равно единице, либо является простым. В противном
случае скрипт производит деление числа на найденный множитель: 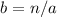 . Для этого, в цикле,
найденная ранее группа единиц, находящаяся в самом начале числа, заменяется на подходящий
маркер (в данном случае используется символ
. Для этого, в цикле,
найденная ранее группа единиц, находящаяся в самом начале числа, заменяется на подходящий
маркер (в данном случае используется символ _). Т.о., по завершению цикла, количество символов подчеркивания равно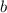 и заменой
и заменой s/_/1/gможно получить этот второй, возможно тоже составной множитель. Множитель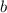 добавляется в список чисел.
добавляется в список чисел.Теперь скрипт рекурсивно обрабатывает найденный множитель
 (пометив его специальным
маркером и начав факторизацию заново) по уже описанной схеме и продолжает процесс, перемащая
маркер к следующему числу в списке при каждой «неудачной» факторизации (т.е. когда
помеченный множитель оказывается простым или равным единице), пока всё исходное число не
окажется разложенным на простые множители.
(пометив его специальным
маркером и начав факторизацию заново) по уже описанной схеме и продолжает процесс, перемащая
маркер к следующему числу в списке при каждой «неудачной» факторизации (т.е. когда
помеченный множитель оказывается простым или равным единице), пока всё исходное число не
окажется разложенным на простые множители.В других диалектах регулярных выражений могут поддерживаться те или иные средства управления жадностью – так в источнике [16] вместо
11+применено подвыражение11+?, которое как раз и указывает механизму сопоставления с образцом действовать нежадно, минимизируя длину найденной подстроки; но в sed таких средств, кажется, нет, а в данном конкретном случае, за счёт рекурсивной обработки всё вновь получаемых множителей, неопределенной жадности вполне достаточно.Интересно, что если для сопоставления с образцом
11+используется гарантированно жадная стратегия, то, коль скоро это соответствует максимизации в разложении
в разложении 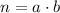 , это
минимизирует
, это
минимизирует 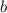 и обеспечивает т.о. его простоту. Данное наблюдение могло бы позволить слегка
сократить и ускорить скрипт, но я не воспользовался такой возможностью (потому что всё и так
работает, да ещё и не зависит от стратегии поиска, выбранной конкретной реализацией регулярных
выражений).
и обеспечивает т.о. его простоту. Данное наблюдение могло бы позволить слегка
сократить и ускорить скрипт, но я не воспользовался такой возможностью (потому что всё и так
работает, да ещё и не зависит от стратегии поиска, выбранной конкретной реализацией регулярных
выражений).Пример работы скрипта:
echo 111111111111111111 | ./factor-hack-unary.sed 111 111 11Так и должно быть:
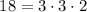 .
. -
euler-sieve.sed– попытка реализации решета Эйлера. Детальное описание приведено в предыдущем разделе. С точки зрения запуска и использования, скрипт должен работать в точности как иsieve.sed(см. выше).
Ссылки
- 1. http://ru.wikipedia.org/wiki/решето_Эратосфена
- 2. https://github.com/Circiter/sieve-in-sed
- 3. http://skerritt.blog/an-algorithm-for-finding-anagrams
- 4. http://quanterocapital.com/anagrams-mathematically-speaking
- 5. http://en.wikipedia.org/wiki/fundamental_theorem_of_arithmetic
- 6. https://gist.github.com/Circiter/042264eb9e9ee360d0eafa10eedf3f21
- 7. http://ru.wikipedia.org/wiki/гипотеза_Коллатца
- 8. Lagarias J. The Ultimate Challenge: the 3x+1 problem. 2010
- 9. http://en.wikipedia.org/wiki/wheel_factorization
- 10. Euler L. Variae observationes circa series infinitas. 1737
- 11. Sorenson J. An Introduction to Prime Number Sieves. 1990
- 12. Gries D. и др. A Linear Sieve Algorithm for Finding Prime Numbers
- 13. http://www.nayuki.io/page/the-versatile-sieve-of-eratosthenes
- 14. http://news.ycombinator.com/item?id=9039537
- 15. http://montreal.pm.org/tech/neil_kandalgaonkar.shtml
- 16. http://www.mit.edu:8008/bloom-picayune.mit.edu/perl/10138