Теория насыщения. Часть I.
Рассматриваются некоторые свойства частичных сумм делителей натуральных чисел и описывается феномен «насыщения» подобных сумм, выражающийся в вытеснении некоторых простых делителей из их факторизаций. Сама исследуемая проблема представляется довольно глубокой и сложной, в силу чего никаких конкретных подтверждённых результатов и полных доказательств, к сожалению, здесь представлено не будет (а имеющиеся рассуждения будут выполнены исключительно элементарными средствами).
Несмотря на ограниченность сообщения констатацией небольшого объёма необходимых дефиниций и эмпирических фактов/догадок вместе с небольшим количеством набросков доказательств (коих, в совокупности, я уже поспешил окрестить «теорией насыщения»), настоящий феномен, я надеюсь, может оказаться интересен любителям теории чисел (впрочем, есть подозрение, что профессиональные математики увидят здесь что-нибудь уже хорошо им известное).
Содержание:
- Вводные замечания
- Некоторые определения
- Основная проблема
- Специальный случай
- Заключение
- Ссылки
Вводные замечания
Изложение придётся начать с оговорок по поводу выбора использующихся далее терминов «насыщенность», «насыщение» и т.д. Поиск в интернете показывает, что в теоретико-числовом контексте понятие насыщенности, так или иначе, изредка употребляется. Где-то это может означать ограниченность набора цифр, использующихся для записи числа (e.g., попадалось определение насыщенного числа, как многоразрядного числа, десятичная запись которого содержит только две цифры, возможно применённых многократно и в произвольной последовательности), а где-то о насыщенности говорят при обсуждении некоторых вариантов машинной арифметики (вроде стандартной реализации чисел с плавающей точкой во многих современных процессорах и языках программирования), в которых при переполнении число «насыщается», приобретая значение ближайшего экстремального значения (вместо «прыжка» в противоположный конец машинной числовой оси как в модулярной арифметике) [1].
Но за исключением эти редких употреблений понятия насыщения числа, термин «насыщенное число» трудно назвать стандартным (ещё раз подчеркну, что трудно именно с точки зрения поверхностного обследования свободно доступных источников при помощи популярных поисковых систем). Поэтому, заметив интересный феномен при проведении кое-каких численных экспериментов, я поспешил использовать это почти свободное слово для введения условно нового термина, именно с целью описания этого феномена в настоящем дневнике. (Если читателям известны более уместные термины, то рад бы был услышать возможные варианты.)
В моём случае, насыщенность будет использоваться для характеризации «состава», т.е. разнообразия простых делителей, довольно специфичных теоретико-числовых объектов, а именно частичных/частных сумм делителей целых чисел (далее я буду сосредоточен на натуральных числах).
Очень похожие проблемы глубоко исследовались Эрдёшем; возможно, знатоки его работ узнают здесь что-нибудь знакомое (e.g. «странные числа» [2]). Хотя, некоторая новизна, я надеюсь, всё-таки остаётся. :)
Некоторые определения
Пусть дано число  . Все его делители образуют множество
. Все его делители образуют множество 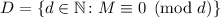 (мощность
(мощность 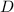 традиционно обозначается
традиционно обозначается 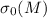 ). На
). На 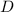 возьмём
какое-нибудь отношение полного порядка
возьмём
какое-нибудь отношение полного порядка 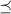 , относительно которого делители будут
упорядочены. В частности, для получения минимального элемента относительно этого отношения будет
использоваться символ
, относительно которого делители будут
упорядочены. В частности, для получения минимального элемента относительно этого отношения будет
использоваться символ 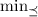 . Если в качестве
. Если в качестве 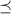 используется обычное отношение
используется обычное отношение
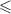 , то будем говорить о каноническом порядке (упорядочивании) делителей.
, то будем говорить о каноническом порядке (упорядочивании) делителей.
Введём последовательность делителей 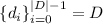 (N.B.
(N.B. 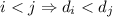 ).
).
Определение
Последовательность частичных сумм делителей обозначим 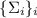 и определим индуктивно:
и определим индуктивно:
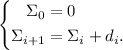
(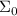 здесь как колёса у рыбы, но, формально, эта частичная сумма соответствует
суммированию по пустому подмножеству делителей; так что пусть пока будет так.)
здесь как колёса у рыбы, но, формально, эта частичная сумма соответствует
суммированию по пустому подмножеству делителей; так что пусть пока будет так.)
В отличии от частичных сумм делителей, сумма всех делителей является очень известным и важным
объектом в теории чисел. Обычно сумму всех делителей числа  обозначают как
обозначают как 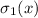 ,
хотя в классической работе Эйлера [3] (см. также перевод с латыни [4]) используется интегралоподобный символ
,
хотя в классической работе Эйлера [3] (см. также перевод с латыни [4]) используется интегралоподобный символ 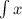 , позволяющий немного
экономить на скобках.
, позволяющий немного
экономить на скобках.
Функция Эйлера 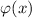 подсчитывает количество чисел, не превышающих
подсчитывает количество чисел, не превышающих  и взаимно простых
с ним. Т.е.
и взаимно простых
с ним. Т.е. 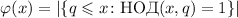 .
.
Определение: Кроме количества чисел, меньших  и взаимно простых с ним, далее может
понадобиться их произведение:
и взаимно простых с ним, далее может
понадобиться их произведение: 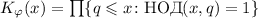 , а
также произведение простых чисел, на которые не делится
, а
также произведение простых чисел, на которые не делится  :
:
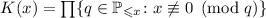 , где
, где 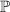 –
множество всех простых чисел.
–
множество всех простых чисел.
Вместо 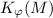 и
и 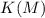 будет писаться просто
будет писаться просто 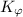 и
и 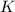 , соответственно. (Связь
, соответственно. (Связь
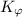 с группами Эйлера могла бы быть важным преимуществом, но пока я буду, в основном,
пользоваться
с группами Эйлера могла бы быть важным преимуществом, но пока я буду, в основном,
пользоваться 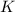 .)
.)
Определение: Введём функцию 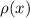 , подсчитывающую количество простых делителей (размер
факторизации) числа
, подсчитывающую количество простых делителей (размер
факторизации) числа  . Пусть
. Пусть 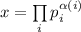 , где
, где 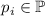 ,
,
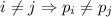 и
и 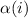 – максимальная степень
– максимальная степень 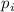 , такая, что
, такая, что
 . Тогда
. Тогда 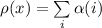 (может быть для неё и
есть какое-нибудь стандартное обозначения, но мне оно не известно).
(может быть для неё и
есть какое-нибудь стандартное обозначения, но мне оно не известно).
Теперь можно приступить к определению насыщенности как таковой.
Определение
Число  назовём слабо насыщенным если
назовём слабо насыщенным если 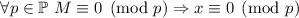 .
.
Другими словами, если обозначить через 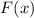 множество различных простых делителей числа
множество различных простых делителей числа  ,
то для слабо насыщенного числа
,
то для слабо насыщенного числа  выполняется
выполняется 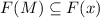 . Т.е. слабо насыщенное число
использует в своей факторизации все факторы числа
. Т.е. слабо насыщенное число
использует в своей факторизации все факторы числа 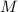 , но, возможно, в других количиствах, и, в
общем случае, в слабо насыщенное число могут входит и другие простые делители, отсутствующие в
факторизации
, но, возможно, в других количиствах, и, в
общем случае, в слабо насыщенное число могут входит и другие простые делители, отсутствующие в
факторизации  .
.
Определение
Число  назовём насыщенным если
назовём насыщенным если 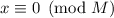 или, что то же самое, если
или, что то же самое, если
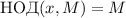 .
.
В факторизации насыщенного числа обязательно присутствуют все факторы числа 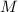 , причём в тех же
степенях (количествах), но могут, кроме этого, быть и другие произвольные факторы.
, причём в тех же
степенях (количествах), но могут, кроме этого, быть и другие произвольные факторы.
Определение
Число  – сильно насыщенно если
– сильно насыщенно если 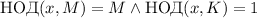 или,
эквивалентно, если
или,
эквивалентно, если 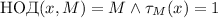 , где функция
, где функция  (не следует путать с
количеством делителей, в этом сообщении обозначаемым через
(не следует путать с
количеством делителей, в этом сообщении обозначаемым через 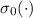 ) определяется через
) определяется через
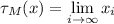 , для последовательности
, для последовательности 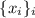 , такой, что
, такой, что
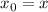 ,
, 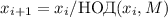 . (Условие
. (Условие 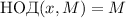 имеет тот же смысл, что
и
имеет тот же смысл, что
и 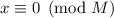 ; также следует заметить, что вместо
; также следует заметить, что вместо 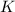 можно было бы использовать
можно было бы использовать
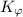 .)
.)
Иначе выражаясь, насыщенное число является сильно насыщенным если в его факторизации нет простых
множителей, не входящих в факторизацию 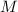 . Сильную насыщенность можно считать обобщённой
гладкостью числа (напомню, что число называют
. Сильную насыщенность можно считать обобщённой
гладкостью числа (напомню, что число называют 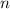 -гладким если оно состоит только из факторов,
не превышающих
-гладким если оно состоит только из факторов,
не превышающих 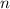 [5]).
[5]).
Примечание: С некоторым риском запутывания терминологии, но ради краткости, далее под ненасыщенным числом будет пониматься число, не обладающее даже свойством слабого насыщения (т.е. у ненасыщенного числа вообще нет никакой разновидности насыщения).
(N.B., введённые выше степени насыщенности определяются относительно зафиксированного 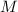 и из
контекста должно быть ясно о каком числе идёт речь, в противном случае рекомендуется делать
уточнения в виде «насыщенность относительно
и из
контекста должно быть ясно о каком числе идёт речь, в противном случае рекомендуется делать
уточнения в виде «насыщенность относительно 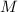 » или, более кратко, «
» или, более кратко, «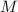 -насыщенность».)
-насыщенность».)
Предложение 1: Эти степени насыщения образуют иерархию в том смысле, что всякое сильно насыщенное число является ещё и насыщенным, а насыщенное число заодно является слабо насыщенным.
О свойствах насыщенных чисел мне известно не так много. Например:
Утверждение 1
- Множество слабо насыщенных чисел замкнуто относительно операций
 и
и  .
.
- Множество насыщенных чисел замкнуто относительно операций
 и
и  .
.
- Сильно насыщенные числа же замкнуты только относительно умножения
 .
.
Набросок доказательства
-
Если числа
 и
и 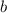 – слабо насыщенны, то факторизация каждого содержит все различные
простые делители числа
– слабо насыщенны, то факторизация каждого содержит все различные
простые делители числа  , и, т.о., можно выделить эту общую часть чисел
, и, т.о., можно выделить эту общую часть чисел  и
и 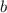 записав их в виде
записав их в виде 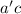 и
и 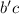 , где число
, где число  при разложении на простые делители будет
содержать все различные делители
при разложении на простые делители будет
содержать все различные делители  и только их. Тогда,
и только их. Тогда, 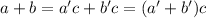 , но число
, но число
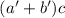 – слабо насыщенно (т.е. делится на каждый из простых делителей числа
– слабо насыщенно (т.е. делится на каждый из простых делителей числа  ).
).Случай с умножением аналогичен: произведение
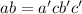 делится на простые делители
делится на простые делители 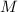 .
. -
Пусть теперь
 и
и 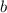 – насыщенные числа. Это значит, что каждое из них делится на
– насыщенные числа. Это значит, что каждое из них делится на  , а
значит, они могут быть представленны в виде
, а
значит, они могут быть представленны в виде  и
и 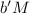 , соответственно. Легко видеть, что
и сумма
, соответственно. Легко видеть, что
и сумма 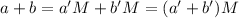 и произведение
и произведение  делятся на
делятся на 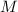 , т.е. тоже
насыщенны.
, т.е. тоже
насыщенны. -
Действуя по той же схеме, запишем произведение cильно насыщенных чисел
 и
и 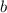 (которые,
автоматически будут и насыщенными) в виде
(которые,
автоматически будут и насыщенными) в виде 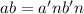 . Видно, что если исходные множители
состояли только из простых делителей числа
. Видно, что если исходные множители
состояли только из простых делителей числа 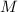 , то в произведении
, то в произведении 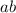 новым простым
делителям взяться неоткуда. а значит
новым простым
делителям взяться неоткуда. а значит 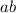 – тоже сильно насыщенное число.
– тоже сильно насыщенное число.N.B., а вот относительно сложения, к сожалению, в общем случае, сильная насыщенность не сохраняется. Действительно, сильно насыщенные числа
 и
и  являются насыщенными, что
позволяет записать их, с использованием того же трюка, что и выше, как
являются насыщенными, что
позволяет записать их, с использованием того же трюка, что и выше, как 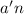 и
и 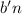 , а их
сумму, соответственно как
, а их
сумму, соответственно как 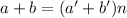 . Но ведь в подвыражении
. Но ведь в подвыражении 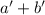 могут запросто
появиться «чужеродные» факторы, нарушающие сильную насыщенность… Ну. в общем,
могут запросто
появиться «чужеродные» факторы, нарушающие сильную насыщенность… Ну. в общем,
 :)
:)
Хотя я и старался ограничиться при изложении лишь элементарными средствами, ближе к концу сообщения понадобится хотя и достаточно элементарный, но глубокий классический (если не сказать древний) результат, больше известный как китайская теорема об остатках (кратко К.Т.О.). Конкретно, ниже приведена конструктивная версия К.Т.О.:
Теорема (без доказательства)
Пусть даны 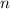 чисел
чисел 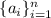 (остатков) и
(остатков) и 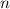 чисел
чисел 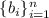 (модулей),
таких, что
(модулей),
таких, что 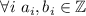 и
и 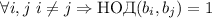 . Тогда система сравнений
. Тогда система сравнений 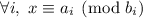 имеет ровно одно решение
имеет ровно одно решение
 , где
, где 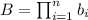 и
и
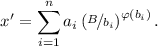
Т.к. 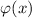 равна количеству чисел, не превышающих
равна количеству чисел, не превышающих  и взаимно простых с
и взаимно простых с  , то при
, то при
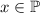 функция Эйлера равна
функция Эйлера равна  (из-за того, что вообще все натуральные
числа из
(из-за того, что вообще все натуральные
числа из 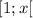 взаимно просты с простым
взаимно просты с простым  ). Это позволяет переписать решение из китайской
теоремы об остатках в виде
). Это позволяет переписать решение из китайской
теоремы об остатках в виде
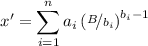
для случая простых модулей
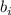 . В настоящем сообщении будет применяться именно это следствие
К.Т.О. для простых модулей.
. В настоящем сообщении будет применяться именно это следствие
К.Т.О. для простых модулей.
Основная проблема
Гипотеза 1
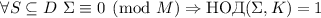 , где
, где
 . Схематично: насыщенность
. Схематично: насыщенность 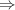 сильная насыщенность.
сильная насыщенность.
Следствие: В частности, 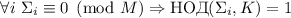 , т.е. из насыщенности некоторой частичной суммы вытекает её сильная насыщенность, причём,
независимо от
, т.е. из насыщенности некоторой частичной суммы вытекает её сильная насыщенность, причём,
независимо от 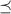 , т.е. для любого порядка включения делителей
, т.е. для любого порядка включения делителей 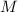 в частичные суммы.
в частичные суммы.
N.B., в гипотезе 1 допустимо не более чем однократное использование каждого из делителей – если некоторый делитель участвует в суммировании многократно, то, вообще говоря, гипотеза может нарушаться.
Некоторые из представленных ниже результатов существенно используют такую последовательность частичных сумм. Более того, некоторые утверждения вместе с их доказательствами подразумевают канонический порядок суммирования делителей. Поэтому, можно сказать, что в этом сообщении не будет почти ничего, касающегося доказательства именно общей гипотезы 1, а, фактически, будут предприниматься попытки обоснования/доказательства лишь следующего частного утверждения:
Гипотеза 2
При каноническом порядке суммирования делителей, выполняется 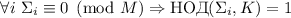 (т.е., по прежнему, сильная насыщенность логически
необходима для насыщенности, но выполнение условия этой гипотезы гарантируется только если
делители упорядочены по возрастанию).
(т.е., по прежнему, сильная насыщенность логически
необходима для насыщенности, но выполнение условия этой гипотезы гарантируется только если
делители упорядочены по возрастанию).
Предложение: Ранее, в предложении 1, было замечено, что степени
насыщения иерархически упорядочены, и, в частности, сильная насыщенность достаточна для
насыщенности. Вместе с утверждаемой в гипотезе 1
необходимостью, это даёт эквивалентность насыщенности и сильной насыщенности: 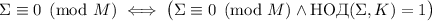 , где
, где 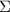 –
сумма по некоторому подмножеству делителей. Очевидно, обе гипотезы 1 и 2 могут быть, при желании,
переформулированы в терминах такой эквивалентности.
–
сумма по некоторому подмножеству делителей. Очевидно, обе гипотезы 1 и 2 могут быть, при желании,
переформулированы в терминах такой эквивалентности.
Рассмотрим небольшой пример. Допустим, 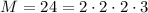 . Множество делителей есть
. Множество делителей есть
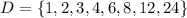 . Произведение простых чисел (меньших
. Произведение простых чисел (меньших 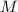 ), на которые
), на которые 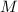 не
делится, равно числу
не
делится, равно числу 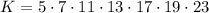 . Частичные суммы
образуют последовательность
. Частичные суммы
образуют последовательность 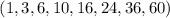 . Непосредственная проверка
показывает, что суммы
. Непосредственная проверка
показывает, что суммы  ,
, 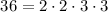 и
и 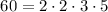 –
слабо насыщенны (в первом случае в факторизации не хватает двух двоек для насыщенности, в
последних двух – не хватает по одной двойке), сумма 24 – насыщенна и к тому же сильно
насыщенна, остальные суммы ненасыщенны.
–
слабо насыщенны (в первом случае в факторизации не хватает двух двоек для насыщенности, в
последних двух – не хватает по одной двойке), сумма 24 – насыщенна и к тому же сильно
насыщенна, остальные суммы ненасыщенны.
Ещё несколько выборочных примеров приведу в виде диаграмм с цветовым кодированием. Жёлтым
покрашены «запрещённые» факторы, присутствующие в частичной сумме делителей, но отсутствующие
в исходном числе 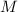 . Синий цвет имеют факторы присутствующие в
. Синий цвет имеют факторы присутствующие в 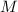 , а также факторы,
находящиеся и в
, а также факторы,
находящиеся и в 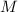 и в частичной сумме одновременно, но не являющиеся критически важными для
насыщенности. Красным цветом обозначены факторы частичной суммы, общие с факторизацией
и в частичной сумме одновременно, но не являющиеся критически важными для
насыщенности. Красным цветом обозначены факторы частичной суммы, общие с факторизацией 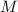 и
важные для присвоения той или иной степени насыщенности данной частичной сумме. Сумма будет
насыщенной если в ней есть все красные факторы из числа
и
важные для присвоения той или иной степени насыщенности данной частичной сумме. Сумма будет
насыщенной если в ней есть все красные факторы из числа 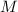 , т.е. если факторизация
, т.е. если факторизация 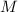 входит в
факторизацию
входит в
факторизацию 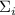 в качестве подпоследовательности. Сумма
в качестве подпоследовательности. Сумма 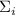 будет сильно
насыщенной если она насыщенна и не имеет жёлтых факторов. Вот некоторые примеры:
будет сильно
насыщенной если она насыщенна и не имеет жёлтых факторов. Вот некоторые примеры:
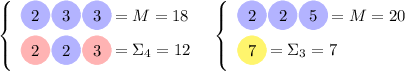
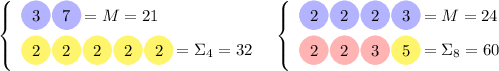

Обратите внимание, как только факторизация 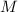 обнаруживается входящей полностью в факторизацию
некоторой
обнаруживается входящей полностью в факторизацию
некоторой 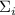 , жёлтые факторы гарантированно вытесняются из факторизации такой частичной
суммы (это показано в двух последних примерах; в примере с
, жёлтые факторы гарантированно вытесняются из факторизации такой частичной
суммы (это показано в двух последних примерах; в примере с 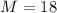 , несмотря на слабое насыщение
частичной суммы
, несмотря на слабое насыщение
частичной суммы 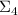 , в ней тоже нет жёлтых факторов, но это лишь совпадение – см. пример
с
, в ней тоже нет жёлтых факторов, но это лишь совпадение – см. пример
с 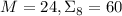 ).
).
Интуитивный смысл гипотезы 2: если некоторая частичная сумма
делится на всё, на что делятся её слагаемые, то она не может делиться ни на что другое, потому,
что сама сумма только из этих слагаемых и состоит. Здесь существенно, что слагаемые – суть
делители числа 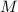 , и без этого ограничения такой эвристический (если не метафизический)
аргумент не работает. Ведь, в общем случае, факторизация суммы может кардинально отличаться от
факторизаций входящих в неё слагаемых; даже просто инкремент числа обычно меняет его
факторизацию до неузнаваемости, в чём, по моему мнению, и лежит основная сложность большинства
задач и открытых проблем теории чисел. А изучение феномена вытеснения лишних факторов — теория
насыщения — может позволить хотя-бы немного разобраться в этом «хаосе» факторизации сумм.
, и без этого ограничения такой эвристический (если не метафизический)
аргумент не работает. Ведь, в общем случае, факторизация суммы может кардинально отличаться от
факторизаций входящих в неё слагаемых; даже просто инкремент числа обычно меняет его
факторизацию до неузнаваемости, в чём, по моему мнению, и лежит основная сложность большинства
задач и открытых проблем теории чисел. А изучение феномена вытеснения лишних факторов — теория
насыщения — может позволить хотя-бы немного разобраться в этом «хаосе» факторизации сумм.
Численные эксперименты вместе с утверждением 1 показывают, что если
гипотеза 2 верна, то её утверждение для 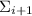 зависит не только от слагаемых
зависит не только от слагаемых  , а для своего доказательства требует учёта
структурных свойств
, а для своего доказательства требует учёта
структурных свойств 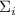 . Поэтому, хотя частичные суммы вводились именно с прицелом на
применение индукции в возможном доказательстве гипотезы, но пока не ясно, будет ли достаточно
этих средств.
. Поэтому, хотя частичные суммы вводились именно с прицелом на
применение индукции в возможном доказательстве гипотезы, но пока не ясно, будет ли достаточно
этих средств.
Утверждение 2: Гипотеза 2
[тривиально] верна для  .
.
Доказательство
У простого числа 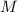 только два делителя, – это 1 и
только два делителя, – это 1 и 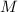 . Соответственно, в этом случае будут
только две ненулевые частичные суммы. При каноническом порядке делителей, сумма
. Соответственно, в этом случае будут
только две ненулевые частичные суммы. При каноническом порядке делителей, сумма 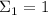 вообще ни на что не делится (кроме единицы, но
вообще ни на что не делится (кроме единицы, но 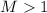 ) и не может быть насыщенной. Сумма
) и не может быть насыщенной. Сумма
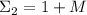 при делении на
при делении на 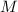 даёт остаток 1 и поэтому тоже не может быть насыщенной. При
другом порядке делителей, сумма
даёт остаток 1 и поэтому тоже не может быть насыщенной. При
другом порядке делителей, сумма 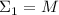 , поэтому она насыщенна (делится на
, поэтому она насыщенна (делится на 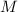 ) и заодно
сильно насыщенна (взаимно проста с
) и заодно
сильно насыщенна (взаимно проста с 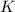 , по определению числа
, по определению числа  ). Следующая сумма
). Следующая сумма
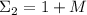 аналогична такой же сумме из уже рассмотренного случая канонического
упорядочивания.
аналогична такой же сумме из уже рассмотренного случая канонического
упорядочивания. 
Похоже, существует какая-то связь между свойствами насыщения частичных сумм делителей, чётностью
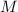 и взаимной простотой
и взаимной простотой 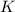 с попарными разностями делителей.
с попарными разностями делителей.
Наблюдение 1: Для нечётных 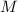 никакая из частичных сумм делителей не достигает насыщения. Эквивалентно:
никакая из частичных сумм делителей не достигает насыщения. Эквивалентно: 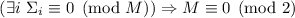 . (Всё это работает только для
канонического порядка делителей: простой контрпример получается если первым делителем выбрать
любой насыщенный делитель, да хоть
. (Всё это работает только для
канонического порядка делителей: простой контрпример получается если первым делителем выбрать
любой насыщенный делитель, да хоть 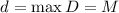 .)
.)
Наблюдение 1 скорее-всего не проще основной гипотезы 2, ведь если для нечётного случая насыщенность вообще не
достигается, то гипотеза выполняется автоматически, больше доказывать нечего. И именно этот
случай 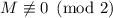 – как назло, самый сложный и интересный. :)
– как назло, самый сложный и интересный. :)
Наивная попытка применить индукцию для доказательства «инварианта» 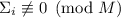 мало к чему приводит: при каконическом порядке делителей базовый случай очевиден (единица ни
на что не делится кроме единицы), самый последний шаг индукции с прибавлением максимального
делителя, равного самому числу
мало к чему приводит: при каконическом порядке делителей базовый случай очевиден (единица ни
на что не делится кроме единицы), самый последний шаг индукции с прибавлением максимального
делителя, равного самому числу 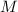 , менее очевиден, но тоже вполне элементарен (я пока не буду
его пояснять, оставляя его в качестве необязательного упражнения читателю :) ). А вот общий шаг
индукции чрезвычайно сложен… По крайней мере у меня ничего не получилось (но попытка
доказательства для достаточно показательного частного случая всё же будет приведена ближе к
концу сообщения) .
, менее очевиден, но тоже вполне элементарен (я пока не буду
его пояснять, оставляя его в качестве необязательного упражнения читателю :) ). А вот общий шаг
индукции чрезвычайно сложен… По крайней мере у меня ничего не получилось (но попытка
доказательства для достаточно показательного частного случая всё же будет приведена ближе к
концу сообщения) .
Наблюдение 2: Для чётных 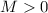 выполняется:
выполняется: 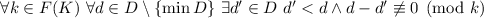 .
.
(Легко видеть, почему наблюдение 2 не выполняется для
нечётных 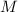 . Раз в факторизации
. Раз в факторизации 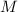 нет двойки, то двоек не будет и в факторизации любого
делителя. Значит, все делители числа
нет двойки, то двоек не будет и в факторизации любого
делителя. Значит, все делители числа 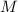 суть нечётные числа, но т.к. разность любых двух
нечётных чисел есть число чётное, то все попарные разности делителей будут делиться на
суть нечётные числа, но т.к. разность любых двух
нечётных чисел есть число чётное, то все попарные разности делителей будут делиться на  и будут контрпримерами (хотя и не единственными).)
и будут контрпримерами (хотя и не единственными).)
Набросок доказательства
Пусть 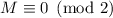 и произвольно выбрано
и произвольно выбрано 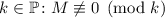 ,
причём
,
причём 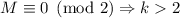 . Доказывается утверждение
. Доказывается утверждение 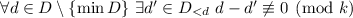 . Доказательство
существования такого
. Доказательство
существования такого 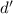 будет проводиться полной индукцией по величине уменьшаемого в
разностях
будет проводиться полной индукцией по величине уменьшаемого в
разностях 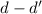 .
.
База:
Т.к. 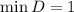 , то
, то 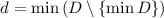 больше единицы, а
т.к.
больше единицы, а
т.к. 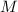 чётно, то базовый случай есть
чётно, то базовый случай есть 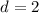 . Поэтому
. Поэтому 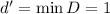 удовлетворяет доказываемому
утверждению. В самом деле,
удовлетворяет доказываемому
утверждению. В самом деле,  т.к.
т.к. 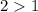 , и
, и 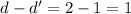 . Очевидно, что раз
. Очевидно, что раз 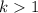 , то
, то
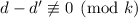 .
.
Предположение индукции: 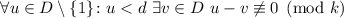 .
.
Шаг индукции:
Пусть 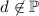 . Тогда
. Тогда 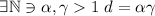 .
Очевидно,
.
Очевидно, 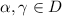 и
и 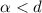 , поэтому, по предположению индукции,
, поэтому, по предположению индукции, 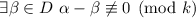 . Остаётся положить
. Остаётся положить 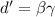 , что даст
разность
, что даст
разность 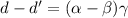 в которой ни
в которой ни  , ни
, ни 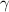 , не делятся на
, не делятся на
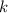 , а значит и
, а значит и 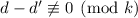 . Вот так вот всё просто для сложных
. Вот так вот всё просто для сложных 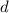 . :)
. :)
А вот для простых 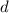 всё, наоборот, сложнее. (Второй раз шутка не срабатывает.) На самом деле,
я не знаю как быть с этой веткой доказательства. А чтобы хоть как-то завершить этот набросок,
могу лишь привести такой полуэвристический аргумент. Пусть
всё, наоборот, сложнее. (Второй раз шутка не срабатывает.) На самом деле,
я не знаю как быть с этой веткой доказательства. А чтобы хоть как-то завершить этот набросок,
могу лишь привести такой полуэвристический аргумент. Пусть 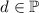 . И предположим, что
всё совсем плохо и
. И предположим, что
всё совсем плохо и  , где
, где 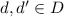 . Попробуем методом от
противного опровергнуть эту пессимистическую возможность отсутствия подходящего
. Попробуем методом от
противного опровергнуть эту пессимистическую возможность отсутствия подходящего 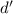 .
.
Пусть 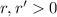 – остатки от деления
– остатки от деления 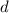 и
и 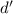 на
на 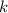 , т.е.
, т.е.  и
и 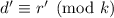 . Вычитая из первого сравнения второе, получаем
. Вычитая из первого сравнения второе, получаем 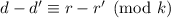 . Что вместе с
предположением
. Что вместе с
предположением  даёт
даёт 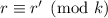 , или просто
, или просто 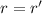 (ведь
(ведь 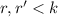 ). Утверждение
). Утверждение 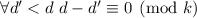 можно поэтому интерпретировать как
можно поэтому интерпретировать как
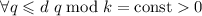 , где
, где 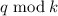 – остаток от деления
– остаток от деления
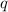 на
на 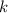 . Т.е. все делители, не превышающие простой делитель
. Т.е. все делители, не превышающие простой делитель 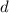 , при делении на
, при делении на 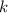 должны
давать одинаковые остатки.
должны
давать одинаковые остатки.
Это не просто звучит удивительно (в конце концов, при нечётном 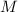 все делители дают один и тот
же остаток по модулю 2, и это, честно говоря, не очень удивляет), но и приводит к более
осязаемым последствиям. А именно, первый, минимальный делитель равен единице и при делении на
все делители дают один и тот
же остаток по модулю 2, и это, честно говоря, не очень удивляет), но и приводит к более
осязаемым последствиям. А именно, первый, минимальный делитель равен единице и при делении на
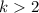 в остатке даёт единицу. Уже следующий делитель, двойка (а он всегда есть, из-за чётности
в остатке даёт единицу. Уже следующий делитель, двойка (а он всегда есть, из-за чётности
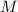 ), даёт при делении на
), даёт при делении на 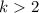 в остатке двойку. Также, каждый последующий простой делитель,
не превышающий
в остатке двойку. Также, каждый последующий простой делитель,
не превышающий 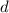 будет, при делении на простое число
будет, при делении на простое число  , давать остаток не меньший двух.
Кратко, это можно записать так:
, давать остаток не меньший двух.
Кратко, это можно записать так:
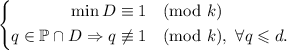
Понятия не имею, можно ли эти рассуждения довести до формального доказательства, но в качестве
подтверждения собственных интуитивных догадок, указанное противоречие (простые делители, не
превышающие 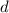 , не сравнимы по модулю
, не сравнимы по модулю 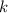 с единицей) меня устраивает. Условно буду считать,
что утверждение
с единицей) меня устраивает. Условно буду считать,
что утверждение 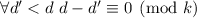 , в свете приведённого аргумента, нарушается
для простых
, в свете приведённого аргумента, нарушается
для простых 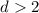 и, соответственно, выполняется
и, соответственно, выполняется 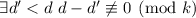 .
(По-настоящему подозрительным в случае с
.
(По-настоящему подозрительным в случае с 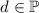 является игнорирование предположения
индукции, но и незаконного здесь ничего нет – методом от противного выводится существование
искомого
является игнорирование предположения
индукции, но и незаконного здесь ничего нет – методом от противного выводится существование
искомого 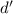 и, т.о., обеспечивается истинность доказываемого утверждения для данного простого
и, т.о., обеспечивается истинность доказываемого утверждения для данного простого
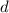 , что делает возможной работу всех будущих шагов индукции.)
, что делает возможной работу всех будущих шагов индукции.)
Всё это могло бы успешно завершить шаг индукции и, как следствие, завершить набросок
доказательства наблюдения 2. 
Специальный случай
Сначала, возможно, стоит попробовать рассмотреть упрощённую версию гипотезы 2, ограничившись числами  , все факторы которых различны (или, лучше
сказать, все факторы или простые делители имеют единичную степень). Т.е., если
, все факторы которых различны (или, лучше
сказать, все факторы или простые делители имеют единичную степень). Т.е., если 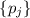 –
последовательность всех простых чисел (
–
последовательность всех простых чисел (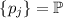 ), то разложение такого
), то разложение такого 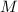 на
простые множители выглядит как
на
простые множители выглядит как 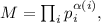 где
где 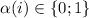 .
Количество различных простых делителей числа
.
Количество различных простых делителей числа  обычно обозначают
обычно обозначают 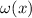 ; с использованием
этого обозначения специальный случай можно охарактировать как
; с использованием
этого обозначения специальный случай можно охарактировать как 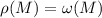 .
.
Последовательностью [модулей] 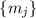 обозначим простые делители числа
обозначим простые делители числа 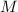 ; чуть выше уже
вводилось обозначение
; чуть выше уже
вводилось обозначение 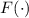 для множества простых делителей, поэтому
для множества простых делителей, поэтому 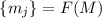 .
Последовательностью же модулей
.
Последовательностью же модулей  обозначим простые числа, меньшие числа
обозначим простые числа, меньшие числа 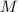 и не делящие
его:
и не делящие
его: 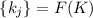 .
.
Количество модулей 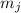 , с использованием ранее придуманной функции
, с использованием ранее придуманной функции 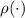 , равно
, равно
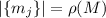 . Очевидно, общее количество модулей
. Очевидно, общее количество модулей 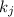 и
и 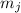 равно
равно 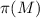 , где
, где 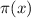 – количество простых чисел, не превышающих
– количество простых чисел, не превышающих  . Тогда количество
модулей
. Тогда количество
модулей  равно
равно 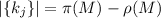 . Напомню также, что
. Напомню также, что
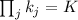 . В рассматриваемом случае с различными факторами в числе
. В рассматриваемом случае с различными факторами в числе 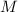 , можно аналогично
записать
, можно аналогично
записать 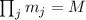 .
.
Гипотеза говорит, что если для некоторого  частичная сумма
частичная сумма 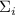 делится на все
делится на все 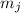 ,
то она не делится ни на один из
,
то она не делится ни на один из 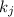 . Я обозвал числа
. Я обозвал числа 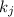 и
и 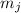 модулями именно потому что
это условие сильного насыщения может быть записано в виде системы сравнений
модулями именно потому что
это условие сильного насыщения может быть записано в виде системы сравнений
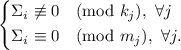
Такая запись интересна хотя-бы потому, что, во-первых, намекает на возможность применения
некоторых интересных результатов теории чисел, вроде китайской теоремы об остатках (например,
К.Т.О. говорит, что, по модулю 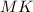 , частичная сумма в левых частях всех этих сравнений
определяется остатками однозначно; из чего следует, если я ничего не напутал, что у двух
частичных сумм [при одном и том же
, частичная сумма в левых частях всех этих сравнений
определяется остатками однозначно; из чего следует, если я ничего не напутал, что у двух
частичных сумм [при одном и том же 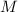 ] не может быть одного и того же вектора остатков), а
во-вторых, подчёркивает удивительность гипотезы 2: делимости
на разные простые числа
] не может быть одного и того же вектора остатков), а
во-вторых, подчёркивает удивительность гипотезы 2: делимости
на разные простые числа 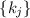 и
и 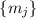 , вроде как, независимы друг от друга, но, тем не
менее, в гипотезе утверждается их строгая скоррелированность – как только остатки от деления на
все
, вроде как, независимы друг от друга, но, тем не
менее, в гипотезе утверждается их строгая скоррелированность – как только остатки от деления на
все 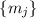 обнуляются, остатки от деления на
обнуляются, остатки от деления на 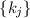 как-то об этом «узнают» и
кооперативно, синхронно становятся ненулевыми.
как-то об этом «узнают» и
кооперативно, синхронно становятся ненулевыми.
Очевидно, достаточно рассматривать лишь случай 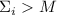 , т.к. если
, т.к. если 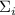 насыщенна,
т.е. если
насыщенна,
т.е. если 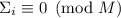 , то
, то 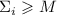 , но при
, но при 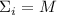 гипотеза
автоматически выполняется (потому что само число
гипотеза
автоматически выполняется (потому что само число 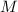 сильно насыщенно).
сильно насыщенно).
Функция 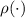 позволяет записать необходимое условие сильной насыщенности в виде
позволяет записать необходимое условие сильной насыщенности в виде
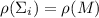 , т.е. переформулировать специальный случай гипотезы как
, т.е. переформулировать специальный случай гипотезы как 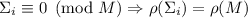 (причём, тривиально выполняется
(причём, тривиально выполняется 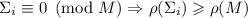 , а вот усиление
, а вот усиление 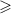 до
до  , – по
видимому, непростая задача).
, – по
видимому, непростая задача).
Раз уж пошло такое хаотичное перечисление первых попавшихся свойств насыщенных частичных сумм (к сожалению без какого бы то ни было приближения к доказательству основной гипотезы), то приведу ещё одно интересное простое наблюдение.
Лемма 1
Если из насыщенной 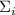 выбросить одно слагаемое, то оставшаяся сумма будет делиться на
это удалённое слагаемое.
выбросить одно слагаемое, то оставшаяся сумма будет делиться на
это удалённое слагаемое.
Доказательство
Насыщенная 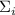 делится на
делится на 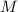 (по определению), а это означает, что
(по определению), а это означает, что 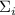 делится на
любой делитель числа
делится на
любой делитель числа 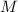 , в частности,
, в частности, 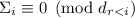 . Делители
. Делители 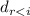 интересны тем, что
интересны тем, что 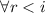 выполняется
выполняется
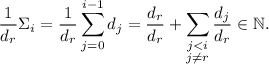
Но такая сумма, очевидно, может быть целым числом только если после вычитания
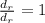 остаётся целая сумма
остаётся целая сумма 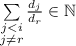 , т.е. если
, т.е. если 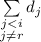 или, что
то же самое,
или, что
то же самое, 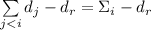 делится на
делится на 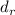 .
. 
Факторизация с двойкой
Если наблюдение 2 выполняется (хотя я и не очень в это
верю), то, возможно, это позволяет немного продвинуться для случая 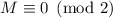 , т.е. для
факторизаций, содержащих двойку.
, т.е. для
факторизаций, содержащих двойку.
Гипотеза 3 (частный случай гипотезы 2)
Если 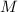 – чётное число, то
– чётное число, то 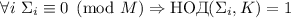 .
.
(Первая версия доказательства писалась для специального случая попарно-различных факторов числа
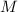 , но потом стало понятно, что без этого требования можно обойтись; так, в нижеслующем
варианте доказательства, кроме делимости на 2, других явных ограничений на факторизацию
, но потом стало понятно, что без этого требования можно обойтись; так, в нижеслующем
варианте доказательства, кроме делимости на 2, других явных ограничений на факторизацию 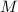 не
накладывается.)
не
накладывается.)
Набросок доказательства
(Предполагается верность [не доказанного окончательно] наблюдения 2.)
Если для некоторого  частичная сумма
частичная сумма 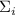 достигла насыщения, то
достигла насыщения, то 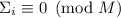 . Из этого следует, что
. Из этого следует, что  и, в частности,
и, в частности,
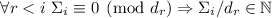 .
.
Дальнейшее доказательство будет вестись от противного, поэтому предположим, что
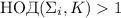 , т.е., что
, т.е., что 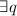 , такое, что
, такое, что 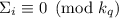 .
.
Т.к. 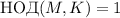 , то
, то 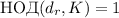 . Поэтому, если в факторизации
. Поэтому, если в факторизации 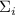 содержится
содержится 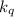 , то после деления
, то после деления 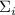 на
на 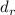 , частное всё-равно будет делиться на
, частное всё-равно будет делиться на
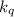 . Т.е. будет выполняться:
. Т.е. будет выполняться:
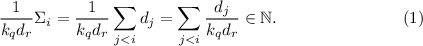
Слагаемое при 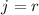 можно вынести в
можно вынести в 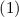 за знак суммирования (cf. лемма 1):
за знак суммирования (cf. лемма 1):

Для целочисленности суммы 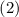 необходимо, чтобы сумма остатков от деления
необходимо, чтобы сумма остатков от деления
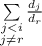 и единицы на
и единицы на 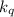 была кратна
была кратна 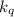 . С
использованием обозначения
. С
использованием обозначения 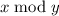 , обозначающего остаток от деления
, обозначающего остаток от деления  на
на 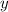 , это условие
можно записать как
, это условие
можно записать как 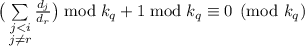 .
.
Т.к. единица не делится на 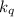 , то первое слагаемое со знаком суммирования тоже не должно
делиться на
, то первое слагаемое со знаком суммирования тоже не должно
делиться на 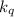 . Также следует заметить, что слагаемое
. Также следует заметить, что слагаемое  не зависит от
не зависит от  . Всё это
приводит к
. Всё это
приводит к  . Если я не ошибаюсь, такое условие можно снова «умножить» на
. Если я не ошибаюсь, такое условие можно снова «умножить» на 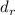 (т.е. умножить обе части лежащего в основе сравнения по модулю
(т.е. умножить обе части лежащего в основе сравнения по модулю 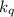 ) и получить выражение
) и получить выражение
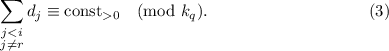
Выражение 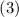 было получено выбрасыванием
было получено выбрасыванием 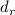 из
из 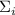 , но этот же процесс
можно повторить и для другого индекса
, но этот же процесс
можно повторить и для другого индекса 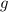 , в результате чего будет получено аналогичное
выражение
, в результате чего будет получено аналогичное
выражение 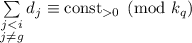 .
Вычитание последнего выражения из
.
Вычитание последнего выражения из 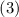 даёт
даёт 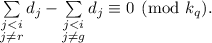 Суммы в левой части этого
сравнения отличаются только наличием/отсутствием слагаемых
Суммы в левой части этого
сравнения отличаются только наличием/отсутствием слагаемых 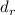 и
и 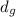 , поэтому после
приведения подобных слагаемых мы получим
, поэтому после
приведения подобных слагаемых мы получим

Если наблюдение 2 верно, то для случая 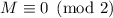 выполняется
выполняется  . Это входит в
противоречие с
. Это входит в
противоречие с 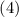 и, т.о., опровергает сделанное ранее предположение о том, что
и, т.о., опровергает сделанное ранее предположение о том, что
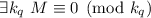 .
. 
Факторизация без двойки и без повторов
Предложение 2 (критерии делителя)
Т.к. число 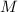 делится на все «разрешённые» модули
делится на все «разрешённые» модули 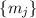 и не делится на «запретные»
модули
и не делится на «запретные»
модули 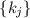 , то любой делитель
, то любой делитель 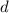 числа
числа 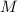 должен делиться хотя-бы на один из модулей
должен делиться хотя-бы на один из модулей
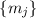 и не должен делиться ни на один из
и не должен делиться ни на один из 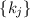 . Если число
. Если число 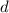 удовлетворяет этим
необходимым критериям, то оно, возможно, является делителем
удовлетворяет этим
необходимым критериям, то оно, возможно, является делителем 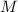 .
.
Иначе говоря, если число  не делится ни на один из
не делится ни на один из 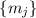 и/или делится на один или
несколько модулей
и/или делится на один или
несколько модулей 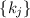 , то
, то 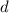 – точно не делитель числа
– точно не делитель числа 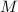 . (В силу очевидности, я
думаю, предложение 2 в доказательстве не нуждается.)
. (В силу очевидности, я
думаю, предложение 2 в доказательстве не нуждается.)
В контексте разбора случая факторизуемости 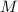 без повторов, стоит уделить особое внимание
наблюдению 1. Напомню, что это наблюдение утверждает, что
для нечётных
без повторов, стоит уделить особое внимание
наблюдению 1. Напомню, что это наблюдение утверждает, что
для нечётных 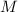 , насыщенных частичных сумм не бывает вообще (при каноническом порядке
делителей). Я до сих пор не знаю как подступиться к этой проблеме, но хотелось бы сделать
следующее «статистическое» замечание о роли нечётности
, насыщенных частичных сумм не бывает вообще (при каноническом порядке
делителей). Я до сих пор не знаю как подступиться к этой проблеме, но хотелось бы сделать
следующее «статистическое» замечание о роли нечётности 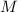 и о возможном подходе к
доказательству. Как я уже говорил ранее, при попытке доказательства по индукции, первый и
последний шаги не представляют трудности и могут пока игнорироваться).
и о возможном подходе к
доказательству. Как я уже говорил ранее, при попытке доказательства по индукции, первый и
последний шаги не представляют трудности и могут пока игнорироваться).
Итак.
Набросок доказательства наблюдения 1
Для «общего» шага индукции, предполагается, что очередная 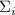 ненасыщенна, т.е. она,
возможно, делится на некоторые из модулей
ненасыщенна, т.е. она,
возможно, делится на некоторые из модулей 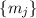 , но совершенно точно не делится на некоторые
другие из них. Нужно показать, что новая сумма
, но совершенно точно не делится на некоторые
другие из них. Нужно показать, что новая сумма 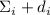 ведёт себя так же и не делится
хотя-бы на один такой модуль.
ведёт себя так же и не делится
хотя-бы на один такой модуль.
Не все комбинации делимостей 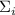 и
и 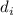 на
на 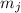 «интересны». Действительно, если из
чисел
«интересны». Действительно, если из
чисел 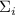 и
и 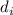 только одно делится без остатка на
только одно делится без остатка на 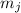 , то результат, новая
частичная сумма
, то результат, новая
частичная сумма 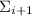 не будет делиться на
не будет делиться на 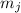 и, т.о., новая частичная сумма
автоматически станет ненасыщенной. Если же оба числа делятся на модуль
и, т.о., новая частичная сумма
автоматически станет ненасыщенной. Если же оба числа делятся на модуль 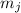 , то новая частичная
сумма
, то новая частичная
сумма 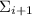 будет делиться на
будет делиться на 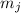 и здесь уже ничего не поделаешь. Интересным
остаётся только случай при котором ни
и здесь уже ничего не поделаешь. Интересным
остаётся только случай при котором ни 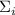 , ни
, ни 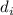 не делятся на
не делятся на 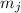 .
.
Именно на этом этапе уместно сделать замечание о возможной роли нечётности  – если
– если  чётно, то
чётно, то 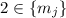 и вышеописанным интересным сравнением может стать сравнение по модулю
и вышеописанным интересным сравнением может стать сравнение по модулю
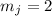 , а именно
, а именно 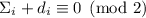 , выполняющемся если
, выполняющемся если 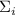 и
и 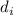 нечётны.
Как видите, интересное сравнение становится неинтересным (результат всегда делится на 2) и
шансы, грубо говоря, распределяются поровну для делимости и неделимости
нечётны.
Как видите, интересное сравнение становится неинтересным (результат всегда делится на 2) и
шансы, грубо говоря, распределяются поровну для делимости и неделимости 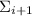 на
на
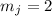 .
.
В то время как при 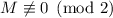 , среди
, среди 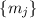 двойки нет, и у сравнения
двойки нет, и у сравнения
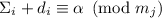 , с некоторой «вероятностью», остаток
, с некоторой «вероятностью», остаток 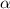 будет
ненулевым и среди всех возможных комбинаций делимостей
будет
ненулевым и среди всех возможных комбинаций делимостей 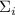 и
и 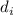 на
на  будет
некоторый статистический перевес в сторону некратности
будет
некоторый статистический перевес в сторону некратности 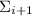 модулю
модулю 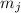 . Заметьте,
что этот аргумент касается только одного сравнения по модулю
. Заметьте,
что этот аргумент касается только одного сравнения по модулю 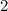 , и мне неизвестно, может ли
всего-лишь это одно сравнение полностью запретить или разрешить насыщенные частичные суммы. Я
лишь поделился самим наблюдением о небольшой асимметрии…
, и мне неизвестно, может ли
всего-лишь это одно сравнение полностью запретить или разрешить насыщенные частичные суммы. Я
лишь поделился самим наблюдением о небольшой асимметрии…
Но вернёмся к разработке стратегии индуктивного доказательства запрета насыщенных частичных сумм
делителей именно нечётного числа 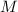 . Итак, мы находимся на одном из промежуточных шагов
индукции,
. Итак, мы находимся на одном из промежуточных шагов
индукции, 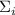 и
и 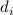 оба не делятся хотя-бы на некоторые модули
оба не делятся хотя-бы на некоторые модули 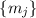 . Более
конкретно, пусть
. Более
конкретно, пусть 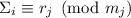 и
и 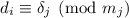 , где остатки
, где остатки
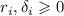 . Сложение этих двух сравнений даёт
. Сложение этих двух сравнений даёт 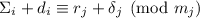 . Допустим, что вопреки ожиданиям и целям,
. Допустим, что вопреки ожиданиям и целям, 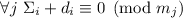 (предположение для опровержения методом «от противного»). Тогда, вычитая из
предпоследнего сравнения последнее получаем
(предположение для опровержения методом «от противного»). Тогда, вычитая из
предпоследнего сравнения последнее получаем 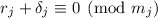 , откуда
, откуда
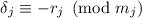 . Вместе с
. Вместе с 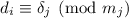 это даёт
это даёт  (если я нигде не ошибся).
(если я нигде не ошибся).
Такую систему (при пробегании индексом  всех допустимых значений) можно решить относительно
всех допустимых значений) можно решить относительно
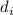 с помощью конструктивной версии К.Т.О. Должно получиться что-то вроде
с помощью конструктивной версии К.Т.О. Должно получиться что-то вроде  , где
, где
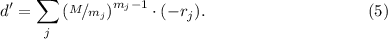
(N.B. Я пишу 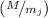 вместо
вместо 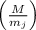 – чтобы
читатель не спутал просто дробь в скобках с каким-нибудь там символом Лежандра. :) )
– чтобы
читатель не спутал просто дробь в скобках с каким-нибудь там символом Лежандра. :) )
Значения полученные с помощью  выглядят подозрительно (слишком большими),
поэтому я решил в качестве решения использовать
выглядят подозрительно (слишком большими),
поэтому я решил в качестве решения использовать 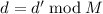 [хотя пока и не знаю как
обосновать законность этого, немного «подгоночного» шага]. Но главная идея здесь заключается в
проверке полученной оценки «делителя»
[хотя пока и не знаю как
обосновать законность этого, немного «подгоночного» шага]. Но главная идея здесь заключается в
проверке полученной оценки «делителя» 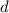 числа
числа 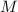 на соответствие её критериям из
предложения 2 – если
на соответствие её критериям из
предложения 2 – если 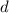 не делится ни на какие модули
не делится ни на какие модули
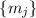 или, наоборот, делится пусть даже на всего один модуль из
или, наоборот, делится пусть даже на всего один модуль из 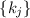 , то это приведёт к
противоречию (т.к. число
, то это приведёт к
противоречию (т.к. число 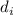 , сравнимое с
, сравнимое с 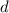 по модулю
по модулю 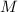 , определённо, по-построению,
является делителем
, определённо, по-построению,
является делителем 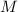 ) и, понятное дело, к опровержению сделанного допущения
) и, понятное дело, к опровержению сделанного допущения
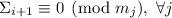 .
.
Находить остаток от деления суммы 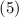 на
на 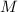 и проверять его делимости на
допустимые
и проверять его делимости на
допустимые 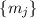 и запрещённые
и запрещённые 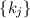 модули страшновато. Но интересно эмпирическое
наблюдение:
модули страшновато. Но интересно эмпирическое
наблюдение:
Наблюдение 3
Для рассматриваемого случая, т.е. для нечётных 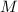 и частичных сумм, отличных от первой,
«аппроксимация»
и частичных сумм, отличных от первой,
«аппроксимация» 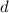 делителя
делителя 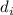 грубо нарушает критерии предложения 2. А именно, эти аппроксимации почему-то не делятся ни на один
грубо нарушает критерии предложения 2. А именно, эти аппроксимации почему-то не делятся ни на один 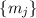 и в
то же самое время делятся хотя-бы на один
и в
то же самое время делятся хотя-бы на один 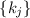 .
.
Критерий с делимостью на модули 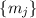 проверить, возможно, проще. Это ощущение основано на
следующем факте.
проверить, возможно, проще. Это ощущение основано на
следующем факте.
Предложение: 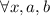 верно
верно 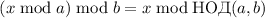 .
.
Доказательство
Действительно, обозначим 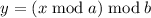 , тогда
, тогда 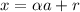 и
и 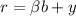 для
некоторых целых
для
некоторых целых 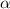 ,
, 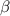 . Также, для целых
. Также, для целых 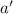 и
и 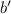 ,
, 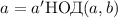 и
и
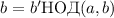 . Подставляя, получаем
. Подставляя, получаем 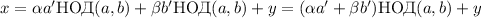 , т.е.
, т.е. 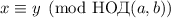 или
или
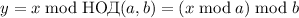 , как и требовалось.
, как и требовалось. 
Т.е., т.к.  , то вместо деления
, то вместо деления 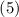 на
на 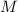 и проверки
делимости полученного остатка на
и проверки
делимости полученного остатка на 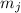 можно ограничиться только нахождением остатка от деления
на
можно ограничиться только нахождением остатка от деления
на 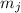 . Тогда результат численных экспериментов можно упростить до
. Тогда результат численных экспериментов можно упростить до
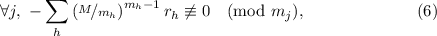
где
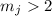 (из-за
(из-за
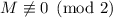 ).
).
Уже не так страшно; но дальше я продвигался очень неуверенно. Непонятно, как формально показать выполнение этого предположения; и непонятно, действительно ли его выполнение будет искомым противоречием…
Что касается первого вопроса (о выполнении условия 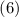 ), то можно попробовать
рассмотреть игрушечный случай лишь с двумя факторами в числе
), то можно попробовать
рассмотреть игрушечный случай лишь с двумя факторами в числе 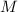 . Итак, пусть
. Итак, пусть  при
при
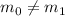 и
и 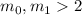 . Ограничимся проверкой условия
. Ограничимся проверкой условия 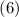 для
для 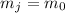 (т.к. ситуация с
(т.к. ситуация с 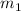 будет полностью аналогичной). Такая проверка тогда сводится к проверке
дробности частного
будет полностью аналогичной). Такая проверка тогда сводится к проверке
дробности частного
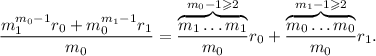
Видно, что из-за
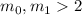 в обоих слагаемых не менее двух множителей в
числителях (возможно роль нечётности
в обоих слагаемых не менее двух множителей в
числителях (возможно роль нечётности  критически важна и здесь). Поэтому один из множителей
критически важна и здесь). Поэтому один из множителей
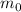 в числителе второй дроби сокращается с
в числителе второй дроби сокращается с 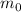 из знаменателя и как минимум один
из знаменателя и как минимум один 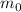 остаётся в числителе, делая эту дробь целой и сводя проверку условия
остаётся в числителе, делая эту дробь целой и сводя проверку условия 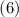 к
проверке нецелочисленности первой дроби. Также видно, что в первой дроби ничего не сокращается
(
к
проверке нецелочисленности первой дроби. Также видно, что в первой дроби ничего не сокращается
(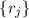 – суть остатки от деления
– суть остатки от деления  на
на 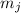 , удовлетворяющие
, удовлетворяющие 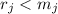 и
в силу этого не могущие сокращаться с
и
в силу этого не могущие сокращаться с 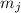 ) и поэтому её значение обязано быть дробным.
) и поэтому её значение обязано быть дробным.
Раз то же самое можно проделать и с делением на 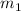 , то приходится заключить, что для частного
случая
, то приходится заключить, что для частного
случая 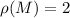 , полученная с помощью К.Т.О. оценка делителей числа
, полученная с помощью К.Т.О. оценка делителей числа 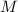 не удовлетворяет
критериям делителя и приводит к противоречию, доказывая (при допущении корректности сделанного
ранее подгоночного шага со взятием остатка по модулю
не удовлетворяет
критериям делителя и приводит к противоречию, доказывая (при допущении корректности сделанного
ранее подгоночного шага со взятием остатка по модулю 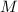 ) наблюдение 1 об отсутствии насыщенных частичных сумм для нечётных
) наблюдение 1 об отсутствии насыщенных частичных сумм для нечётных 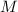 .
.
Для более общего случая 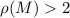 всё немного сложнее (но схема та же). Для проверки делимости
выражения из
всё немного сложнее (но схема та же). Для проверки делимости
выражения из 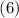 , разделим его на
, разделим его на 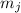 и разложим сумму, выделив в ней одно
слагаемое:
и разложим сумму, выделив в ней одно
слагаемое:
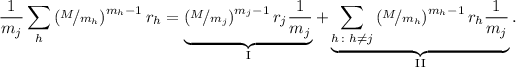
(Минус перед суммой выброшен, т.к. он никак не влияет на целочисленность.)
Т.к. рассматривается случай 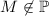 (для простых
(для простых 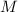 справедливо утверждение 2), то у числа
справедливо утверждение 2), то у числа 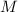 больше двух простых делителей, что приводит к
неравенству нулю обоих подвыражений
больше двух простых делителей, что приводит к
неравенству нулю обоих подвыражений 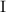 и
и  (хотя, обращаться к утверждению 2 необязательно – если всё-таки
(хотя, обращаться к утверждению 2 необязательно – если всё-таки  , то подвыражение
, то подвыражение
 , и только оно, обратится в ноль, но т.к. ноль есть число целое, то подвыражение
, и только оно, обратится в ноль, но т.к. ноль есть число целое, то подвыражение
 всё-равно никак не повлияет на дробность или целочисленность всей суммы подвыражений
всё-равно никак не повлияет на дробность или целочисленность всей суммы подвыражений
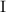 и
и  ).
).
Сначала проанализируем подвыражение  более подробно. В каждом слагаемом разделим
более подробно. В каждом слагаемом разделим 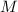 на
на 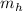 . Т.к.
. Т.к. 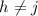 и степень, в которую возводится каждое слагаемое, не меньше двух (из-за
нечётности
и степень, в которую возводится каждое слагаемое, не меньше двух (из-за
нечётности 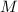 ), то
), то 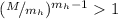 и один из этих
и один из этих 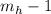 множителей можно
будет поделить на
множителей можно
будет поделить на 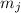 , в результате чего в знаменателе вообще ничего не останется, и текущее
слагаемое, — а значит и вся сумма
, в результате чего в знаменателе вообще ничего не останется, и текущее
слагаемое, — а значит и вся сумма  , — будет целым числом, из-за чего подвыражение
, — будет целым числом, из-за чего подвыражение
 можно в дальнейшем игнорировать.
можно в дальнейшем игнорировать.
Теперь, по-аналогии, перейдём к подвыражению 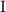 . Деление
. Деление 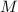 на
на 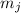 вычеркивает фактор
вычеркивает фактор
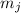 из
из 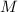 . Поэтому, подвыражение
. Поэтому, подвыражение  можно преобразовать в
можно преобразовать в
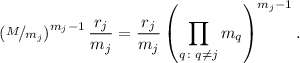
В произведении, возведённом в степень, можно перегруппировать множители, и тогда подвыражение
 запишется как
запишется как 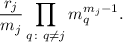
Видно, что из-за
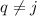 , вся формула представляет собой дробь, числитель
которой – целое число, не содержащее фактора
, вся формула представляет собой дробь, числитель
которой – целое число, не содержащее фактора 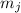 (
(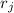 – есть остаток от деления
– есть остаток от деления 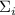 на
на 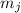 , т.е.
, т.е. 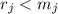 и, следовательно, тоже не может содержать фактор
и, следовательно, тоже не может содержать фактор 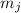 ), а в
знаменателе находится
), а в
знаменателе находится 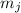 . Такая дробь не может быть целой.
. Такая дробь не может быть целой.
Опять получили нарушение предложения 2, а значит и противоречие, доказывающее наблюдение 1.
Строго говоря, чтобы завершить эту попытку доказательства наблюдения 1, понадобится описать ещё базовый случай. При каноническом, возрастающем
порядке следования делителей, база индукции будет соответствовать случаю 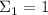 . Он
очевиден, т.к.
. Он
очевиден, т.к. 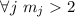 и поэтому
и поэтому 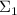 не делится ни на какой из
не делится ни на какой из 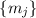 , т.е.
, т.е.
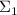 – не является насыщенной.
– не является насыщенной.
(Последний шаг интересен сам по себе. Для него, опять же при каноническом порядке делителей,
очередной добавляемый делитель равен самому числу 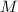 , т.е. следующая сумма выглядит как
, т.е. следующая сумма выглядит как
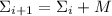 , где
, где 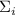 , по предположению индукции, ненасыщенна, т.е. не
делится на
, по предположению индукции, ненасыщенна, т.е. не
делится на 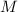 . Неделимость на
. Неделимость на 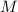 означает, что
означает, что 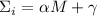 для некоторых
для некоторых
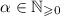 и
и 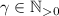 . Тогда
. Тогда 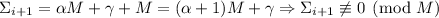 .)
.)
Набросок доказательства наблюдения 1 для частного случая
факторизации без повторов завершён. 
И на этой ноте, первую часть вводного мини-отчёта об основах «теории насыщения» я пока прерву. :)
Заключение
Я не знаю, смогут ли приведённые в этом сообщении интуитивные доводы и экспериментальные наблюдения лечь в основу полноценного доказательства феномена из гипотезы 2. Но, надеюсь, я смог поделиться с читателями моей заинтересованностью в «теории насыщения». Феномен, лежащий в основе этой небольшой теории, имеет и самостоятельную ценность и, потенциально, может иметь «прикладное» значение в других задачах теории чисел.
Рассуждения, в основном, проводились для весьма частного случая разложимости данного числа на
простые множители без повторов. Особых, принципиальных препятствий для обобщения на произвольные
числа пока не видно. (Действительно, что если вместо простых  брать взаимно простые модули
вида
брать взаимно простые модули
вида  из канонического разложения
из канонического разложения 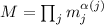 , где
, где
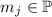 и
и 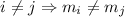 ? Китайская теорема об остатках прекрасно
работает с такими модулями; другие фрагменты рассуждений тоже потенциально могут быть
адаптированы к взаимно простым модулям вместо простых… Осталось аккуратно переписать всё для
этого наиболее общего случая, но желательно после «отладки» имеющейся схемы рассуждений; вдруг
там слишком много ошибок?)
? Китайская теорема об остатках прекрасно
работает с такими модулями; другие фрагменты рассуждений тоже потенциально могут быть
адаптированы к взаимно простым модулям вместо простых… Осталось аккуратно переписать всё для
этого наиболее общего случая, но желательно после «отладки» имеющейся схемы рассуждений; вдруг
там слишком много ошибок?)
Предварительные итоги: наблюдения 1, 2, а также гипотезы 1, 2 и 3 выполняются для всех
чисел, до которых я только смог и захотел дотянуться. :) Возможно, хотя я и не уверен, что из
наблюдения 1 и гипотезы 3 выводится гипотеза 2 (все связи уже были показаны в этом
сообщении; наблюдение 1 покрывает случаи нечётных 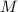 ,
гипотеза 3 – чётных). Ну а сама гипотеза 2 может обобщать некоторые интересные вещи из теории чисел (правда, утверждать
это наверняка, тоже пока преждевременно).
,
гипотеза 3 – чётных). Ну а сама гипотеза 2 может обобщать некоторые интересные вещи из теории чисел (правда, утверждать
это наверняка, тоже пока преждевременно).
Гипотеза 1 остаётся открытой, хотя для моих нужд вполне достаточно и гипотезы 2.
Идеи и вопросы из теории насыщения не ограничиваются изложенными в этом документе, и, вероятно, вскоре я напишу вторую часть, рискуя ещё больше озадачить читателя любительскими набросками доказательств, но попытаюсь при этом сделать акцент именно на приложениях теории.
Обновление (август, 2021): Я написал продолжение, вторую часть этой серии сообщений. Среди прочего, там, в приложении после списка литературы, размещена «заплатка», позволяющая обобщить результаты, полученные ранее для специального случая равенства степеней факторов единице. По крайней мере, теперь в наличии есть все фрагменты, необходимые для написания [наброска] полного доказательства гипотезы 2. Ситуация с идейной и технической корректностью рассуждений, впрочем, всё так же не прояснилась. :)
Ссылки
- 1. http://en.wikipedia.org/wiki/saturation_arithmetic
- 2. Stan B. и др. On Weird and Pseudoperfect Numbers. 1974
- 3. Euler L. Observation de summis divisorum. 1760 http://eulerarchive.maa.org/backup/E243.html
- 4. Euler L. An observation on the sums of divisors / пер. Bell J. 2009 http://arxiv.org/abs/math/0411587
- 5. http://en.wikipedia.org/wiki/smooth_number