Теория насыщения. Часть II.
Сообщение является продолжением серии «теория насыщения». В первой части были заложены основы теории, изучающей интересный феномен «насыщения» факторизаций частичных сумм делителей. В том числе, был приведён ряд гипотез и наблюдений вместе со схематичными попытками их доказательств. Но почти ничего не было сказано о возможных применениях этих несколько спекулятивных результатов.
Теория насыщения (если она не ошибочна) призвана разрешить некоторые конфликты между аддитивными и мультипликативными аспектами теории чисел, и, похоже, что феномен насыщения позволяет приблизится к решению некоторых давних сложных задач, среди которых и широко известная гипотеза о несуществовании нечётных совершенных чисел (конкретно, к концу сообщения приводятся два доказательства отсутствия нечётных совершенных чисел; естественно, выполненные исходя из предположения о верности основных результатов теории насыщения).
Содержание:
- Введение
- Определения и старые результаты
- Новые вспомогательные результаты
- Практическое применение
- Заключение
- Ссылки
- Приложение A
Введение
Я рад, что читатель не сбежал после прочтения аннотации. :) Да, задаче о нечётных совершенных числах около двух килолет, и её до сих пор официально не решили. Общепринятая гипотеза гласит, что таких чисел попросту не существует, и именно эта гипотеза будет основных объектом для «клинических испытаний» теории насыщения.
Рекомендуется ознакомиться с первой частью [1] этой серии сообщений. В ней описаны основы этой небольшой теории, даются необходимые определения. Основным результатом проведённых изысканий является ряд гипотез и наблюдений вместе с набросками их доказательств (по крайней мере, для интересного частного случая).
(Формат этих заметок не подразумевает использования неудобных перекрёстных ссылок между сообщениями. Поэтому основные результаты и определения я кратко повторю здесь.)
Определения и старые результаты
Кое-какие обозначения
-
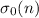 – количество всех делителей числа
– количество всех делителей числа 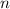 ;
;
-
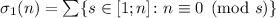 – сумма всех делителей числа
– сумма всех делителей числа 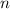 ;
;
-
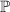 – множество всех простых чисел;
– множество всех простых чисел; -
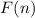 – множество различных простых делителей числа
– множество различных простых делителей числа 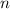 ;
;
-
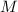 – произвольное число, относительно которого по-умолчанию рассматриваются многие
результаты теории насыщения;
– произвольное число, относительно которого по-умолчанию рассматриваются многие
результаты теории насыщения; -
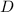 – множество делителей числа
– множество делителей числа 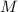 (N.B.,
(N.B., 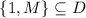 );
);
-
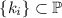 – различные простые числа («запрещённые модули»), меньшие числа
– различные простые числа («запрещённые модули»), меньшие числа
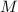 и взаимно простые с ним;
и взаимно простые с ним; -
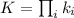 – число, факторизация которого образована всеми числами
– число, факторизация которого образована всеми числами 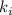 (N.B., все
факторы различны).
(N.B., все
факторы различны).
Определения
- Число
 – слабо насыщенно если
– слабо насыщенно если 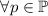 выполняется импликация
выполняется импликация 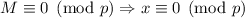 ;
;
- Число
 – насыщенно если
– насыщенно если 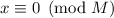 ;
;
- Число
 – сильно насыщенно если
– сильно насыщенно если 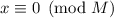 и
и 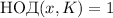 ;
;
- Делители числа
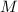 составляют множество
составляют множество 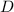 , а будучи упорядоченными некоторым образом,
образуют последовательность
, а будучи упорядоченными некоторым образом,
образуют последовательность 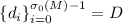 ;
;
- Отношение порядка по-умолчанию для множества
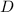 есть
есть 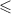 , и если делители
, и если делители 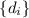 упорядочены относительно
упорядочены относительно 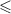 , т.е., упорядочены по возрастанию, то говорят о
каноническом порядке делителей;
, т.е., упорядочены по возрастанию, то говорят о
каноническом порядке делителей; - Частичные суммы делителей числа
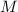 образуют последовательность
образуют последовательность 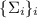 , заданную
рекуррентно:
, заданную
рекуррентно:  .
.
Гипотеза 1
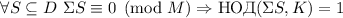 (из
насыщенности следует сильная насыщенность).
(из
насыщенности следует сильная насыщенность).
Из 1 вытекает утверждение о логической необходимости сильной насыщенности и для насыщения частичных сумм делителей, независимо от порядка включения делителей в сумму. По факту, некоторые из приведённых в предыдущем сообщении набросков доказательств, подразумевают канонический порядок делителей. Так что, главным инструментом (и основным объектом попыток доказательства) в текущей версии теории насыщения является следующее утверждение:
Гипотеза 2
При каноническом порядке суммирования делителей, справедливо 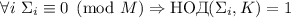 .
.
Наблюдение 1
Для нечётных 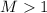 , при каноническом порядке делителей, ни одна из частичных сумм не достигает
насыщения:
, при каноническом порядке делителей, ни одна из частичных сумм не достигает
насыщения: 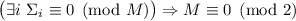 .
.
Наблюдение 2
Для чётных 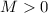 справедливо
справедливо 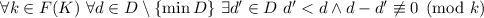 .
.
Примерная словесная формулировка: для произвольного, заранее выбранного запрещённого модуля 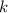 ,
среди попарных разностей делителей числа
,
среди попарных разностей делителей числа 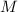 «много» разностей, не делящихся на
«много» разностей, не делящихся на 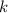 , а именно,
если выбрать какой-нибудь неминимальный (не равный единице) делитель, то найдётся меньший
делитель, такой, что разность между этими двумя делителями не будет кратна
, а именно,
если выбрать какой-нибудь неминимальный (не равный единице) делитель, то найдётся меньший
делитель, такой, что разность между этими двумя делителями не будет кратна 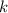 .
.
Гипотеза 3
Если 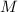 – чётное, то
– чётное, то 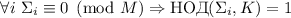 .
.
Связи между утверждениями
Ключевые утверждения (гипотезы 1, 2 и 3, наблюдения 1 и 2) и связи между ними
представлены на диаграмме ниже:
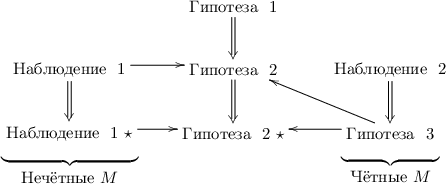
В левом столбце размещены утверждения для нечётных  , в правом – для чётных.
, в правом – для чётных.
Звёздочками  помечены версии утверждений, сделанные в предположении попарного различия
всех простых множителей в разложении
помечены версии утверждений, сделанные в предположении попарного различия
всех простых множителей в разложении  (у всех факторов единичные степени). Стрелками
(у всех факторов единичные степени). Стрелками
 помечены обычные логические импликации,
помечены обычные логические импликации, 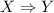 означает, что из
утверждения
означает, что из
утверждения 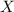 следует утверждение
следует утверждение 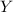 .
.
Стрелки же  (могущие быть заменёнными на
(могущие быть заменёнными на  ) позволяют показать, как одно
утверждение вносит вклад в доказательство другого:
) позволяют показать, как одно
утверждение вносит вклад в доказательство другого: 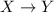 означает, что утверждение
означает, что утверждение 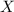 ,
возможно наряду с другими утверждениями, «вносит вклад» в утверждение
,
возможно наряду с другими утверждениями, «вносит вклад» в утверждение 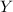 – к примеру,
доказательство утверждения
– к примеру,
доказательство утверждения 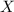 может входить, в качестве фрагмента, в доказательство
может входить, в качестве фрагмента, в доказательство 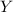 ;
понятно, что утверждение
;
понятно, что утверждение 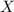 в этом случае обычно логически необходимо для утверждения
в этом случае обычно логически необходимо для утверждения 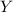 , т.е.
, т.е.
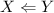 . Ну, может быть, это и не самые удачные обозначения… :)
. Ну, может быть, это и не самые удачные обозначения… :)
Новые вспомогательные результаты
Гипотеза 4 (следствие гипотезы 2)

Доказательство
Множество 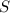 состоит из натуральных чисел, не делящихся на простое
состоит из натуральных чисел, не делящихся на простое 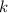 . Гипотеза утверждает,
что если все элементы
. Гипотеза утверждает,
что если все элементы 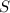 – суть делители максимума
– суть делители максимума 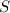 , то сумма всех элементов
, то сумма всех элементов 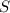 не равна
не равна
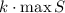 .
.
Положим 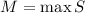 . Пусть множество всех делителей есть
. Пусть множество всех делителей есть 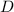 . Т.к. элементы
. Т.к. элементы 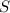 не делятся на
не делятся на
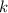 , то максимальный элемент, M, не делится на
, то максимальный элемент, M, не делится на 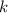 ; следовательно, ни один из элементов
; следовательно, ни один из элементов 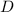 не
делится на
не
делится на 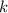 . Упорядочим все делители в возрастающую последовательность
. Упорядочим все делители в возрастающую последовательность  .
Очевидно,
.
Очевидно, 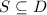 . Теперь образуем частичные суммы
. Теперь образуем частичные суммы 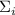 делителей
делителей 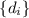 по
правилу
по
правилу 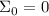 и
и 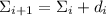 .
.
Т.к. 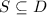 , то
, то 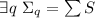 . Число
. Число 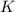 определяется как обычно. При
этом выполняется
определяется как обычно. При
этом выполняется 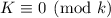 , т.е.
, т.е. 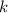 присутствует в разложении
присутствует в разложении 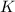 на простые
множители. Все эти условия делают применимой гипотезу 2. Она
утверждает, что
на простые
множители. Все эти условия делают применимой гипотезу 2. Она
утверждает, что 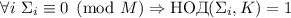 . В
частности, т.к.
. В
частности, т.к. 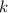 входит в факторизацию
входит в факторизацию 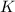 , то
, то
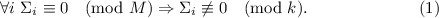
Теперь можно завершить доказательство, воспользовавшись методом от противного. Пусть
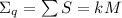 . Из этого следует, что
. Из этого следует, что 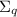 – насыщенна относительно
– насыщенна относительно 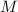 , т.е.
, т.е.
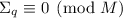 . Но
. Но 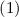 говорит, что
говорит, что 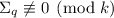 .
Противоречие.
.
Противоречие. 
Лемма 1 (следствие гипотезы 4)
Пусть  и
и  , такое, что
, такое, что  . Пусть также
. Пусть также
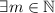 , такое, что
, такое, что 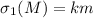 . Тогда
. Тогда 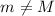 .
.
Доказательство
Предположим, что 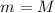 , откуда
, откуда  .
.
Пусть 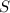 – множество делителей числа
– множество делителей числа 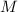 . Тогда
. Тогда

Заметим, что
 , ведь
, ведь 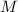 является своим делителем. При этом, очевидно,
является своим делителем. При этом, очевидно, 
и, по построению,
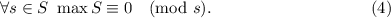
Т.к., по условию, 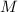 не делится на простое
не делится на простое 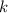 , т.е.
, т.е. 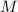 не содержит
не содержит 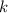 в своей факторизации,
то в сумме
в своей факторизации,
то в сумме 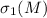 всех делителей
всех делителей 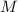 ни одно из слагаемых не делится на
ни одно из слагаемых не делится на 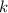 , и,
соответственно, ни один элемент множества
, и,
соответственно, ни один элемент множества 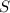 тоже не кратен
тоже не кратен 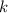 ; другими словами
; другими словами

Свойства 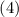 и
и 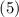 , означают, что ко множеству
, означают, что ко множеству 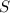 ,
при данном
,
при данном 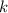 , применима гипотеза 4. Её заключение
утверждает, что
, применима гипотеза 4. Её заключение
утверждает, что 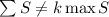 , откуда следует, учитывая равенства
, откуда следует, учитывая равенства 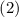 и
и
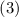 , что
, что  . Противоречие.
. Противоречие. 
Практическое применение
Нечётные совершенные числа
Определение
Число 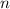 , такое, что
, такое, что 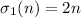 , называется совершенным числом (половина суммы всех
делителей совершенного числа равна самому числу) [2,3].
, называется совершенным числом (половина суммы всех
делителей совершенного числа равна самому числу) [2,3].
Гипотеза 5
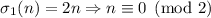 . Т.е. предполагается, что не существует нечётных
совершенных чисел.
. Т.е. предполагается, что не существует нечётных
совершенных чисел.
Примечание
Иногда эту гипотезу называют гипотезой Эйлера, но весьма условно, в том смысле, что она восходит аж к Никомаху Герасскому (circa 100 лет до н.э.), см. переводы [4,5]. Более того, сам я точно не знаю, в какой именно из своих работ Эйлер высказывался о возможном несуществовании нечётных совершенных чисел (как только узнаю, сразу добавлю ссылку в список литературы).
В XIX веке, Сильвестер приводил известный эвристический аргумент [6] — «сеть Сильвестра» — в пользу несуществования нечётных совершенных чисел. Он апеллировал к слишком малой вероятности одновременного удовлетворения нечётным совершенным числом всем известным ограничениям (а их накопилось немало) на возможный вид таких гипотетических объектов.
В конце XX – начале XXI века появился теперь широко известный эвристический аргумент Померанса
[7]. Сначала Карл Померанс вспоминает результат Эйлера о том, что
нечётное совершенное 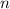 должно иметь вид
должно иметь вид 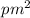 , где
, где 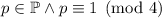 .
Т.к.
.
Т.к. 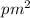 делится на
делится на 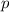 , Померанс замечает, что
, Померанс замечает, что 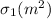 должна делиться на
должна делиться на 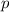 . Из
определения совершенного числа также вытекает, что
. Из
определения совершенного числа также вытекает, что 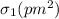 должна делиться на
должна делиться на 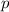 .
Отсюда делается вывод об ограниченности количества таких
.
Отсюда делается вывод об ограниченности количества таких 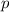 логарифмом от
логарифмом от 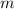 и о том, что
вероятность делимости
и о том, что
вероятность делимости 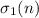 на
на 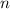 равна
равна 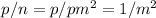 . Вероятность же того, что
хотя-бы одно число
. Вероятность же того, что
хотя-бы одно число 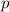 подойдёт равна
подойдёт равна 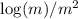 . Из сходимости суммы
. Из сходимости суммы 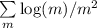 делается вывод о существовании лишь конечного количества нечётных совершенных
чисел.
делается вывод о существовании лишь конечного количества нечётных совершенных
чисел.
Далее Померанс обращается к фактическим результатам поиска таких чисел. Из того, что искомых
чисел, меньших 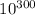 не обнаружено, и из того, что для нечётных совершенных чисел, больших
не обнаружено, и из того, что для нечётных совершенных чисел, больших
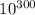 должно выполняться
должно выполняться 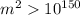 , Померанс приходит к тому, что на самом деле лучше
рассматривать сумму
, Померанс приходит к тому, что на самом деле лучше
рассматривать сумму 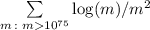 (как я понимаю, из-за того,
что
(как я понимаю, из-за того,
что 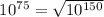 ) и, численно оценив эту сумму как не превышающую
) и, численно оценив эту сумму как не превышающую 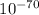 ,
делает заключение о слишком малой вероятности существования нечётных совершенных чисел и даже
сразу усиливает его до несуществования таких чисел.
,
делает заключение о слишком малой вероятности существования нечётных совершенных чисел и даже
сразу усиливает его до несуществования таких чисел.
В общем, очень многие верили и верят (но не все; Декарт, возможно, являлся важным исключением) в то, что существуют только чётные совершенные числа (причём, фактически, аргумент Померанса применим и к чётным совершенных числам тоже, так что, хотя они и существуют, но их количество, возможно, конечно). И аргументы Сильвестра и Померанса делают справедливость гипотезы 5 весьма вероятной.
Я же собираюсь применить к гипотезе 5 строящуюся теория насыщения. :)
Доказательство гипотезы 5
Пусть произвольное нечётное 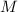 таково, что
таково, что 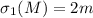 для некоторого
для некоторого
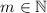 . К этому случаю применима лемма 1 при
. К этому случаю применима лемма 1 при 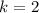 . Она говорит, что
. Она говорит, что 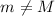 . А из
произвольности выбора нечётного
. А из
произвольности выбора нечётного 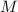 следует, что ни одно нечётное
следует, что ни одно нечётное 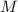 не может удовлетворять
уравнению
не может удовлетворять
уравнению 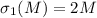 , т.е. не может быть совершенным. Иначе говоря, все совершенные числа
являются чётными.
, т.е. не может быть совершенным. Иначе говоря, все совершенные числа
являются чётными. 
Это доказательство опиралось на гипотезу 2 (или более общую гипотезу 1), утверждающую, что из насыщенности следует сильная насыщенность. Но так получилось, что наблюдение 1 об отсутствии насыщенных сумм делителей нечётных чисел может использоваться для упрощённого доказательства гипотезы 5 напрямую (т.е., на текущий момент, теория насыщения включает в себя больше чем требуется для доказательства отсутствия нечётных совершенных чисел).
Определение: 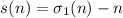 – сумма собственных делителей числа
– сумма собственных делителей числа 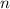 (ещё её
называют аликватной суммой).
(ещё её
называют аликватной суммой).
Доказательство 2 гипотезы 5
Очевидно, совершенные числа могут быть определены как неподвижные точки функции 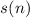 . Так если
некоторое нечётное
. Так если
некоторое нечётное 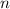 является неподвижной точкой
является неподвижной точкой  , то выполняется
, то выполняется 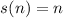 , откуда
, откуда
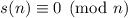 . Но наблюдение 1 говорит, что для
нечётного
. Но наблюдение 1 говорит, что для
нечётного 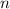 никакая частичная сумма делителей, в т.ч. и аликватная сумма, не может быть
насыщенной и, соответственно, не может делиться на
никакая частичная сумма делителей, в т.ч. и аликватная сумма, не может быть
насыщенной и, соответственно, не может делиться на 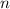 . Противоречие.
. Противоречие. 
Эйлер показал, что у нечётных совершенных чисел один фактор должен иметь степень, сравнимую с единицей по модулю 4, остальные – чётные степени. Поэтому, рассмотренного в предыдущем сообщении специального случая факторизации без повторов, при которой все степени нечётны и равны единице, явно не достаточно для применения к гипотезе 5 (хотя в заключительной части того сообщения я указал на возможный путь обобщения).
Выше я продемонстрировал возможный подход к проблеме нечётных совершенных чисел. И как только общее доказательство гипотезы 2 будет готово, это сразу же будет означать, что действительно не существует ни одного нечётного совершенного числа. :)
В приложении A может быть найдена заплатка, обеспечивающая искомое обобщение выполненного ранее доказательства наблюдения 1. Неявно подразумевается, что адаптация других доказательств из первой части этой серии сообщений, тоже может быть выполнена без особых трудностей или же вовсе не требуется.
Заключение
Сам срок, прошедший с выхода «Введения в арифметику» Никомаха из Герасы, превысивший уже две тысячи лет, намекает на некоторую подозрительность моего результата.
Вероятностный аргумент Померанса так и вовсе есть образец неоднозначности типа «стакан полон versus стакан пуст» – можно делать акцент на исчезающе малой вероятности и, соответственно, делать вывод о несуществовании нечётных совершенных чисел (даже несмотря, ещё раз повторюсь, на потенциальную применимость этого аргумента к чётным совершенным числам при их явном существовании), а можно обратить внимание на возможное не равенство этой вероятности нулю и сделать вывод (противоположный!) о их возможном существовании, – хотя, в то же самое время, подходящая вариация аргумента Померанса, по-видимому, могла бы оказаться ценной для обоснования гипотезы о конечности всех совершенных чисел.
Таким образом, убедительной независимой поддержки верности или ошибочности моего доказательства мне найти не удалось. Но сам феномен насыщения не становится от этого менее интересным.
Вопросы и задачи, остающиеся пока открытыми:
- Верна ли гипотеза 1? Я лишь высказал её, но de facto вместо неё доказывал и применял гипотезу 2;
- Каковы другие возможные применения теории насыщения?
- Потенциально интересной целевой задачей для настоящей теории мог бы стать [тоже пока открытый] вопрос о конечности количества совершенных чисел вообще (т.е. чётных, раз нечётных скорее-всего не существует). Но пригоден ли этот математический аппарат для решения задач такого рода?
- Можно временно проигнорировать возраст «гипотезы Никомаха-Эйлера», вспомнив, что теорема Гёделя о неполноте появилась только в веке XX, и задаться вопросом, а не обусловлено ли перманентное ускользания нечётных совершенных чисел от попыток их поиска именно подобными явлениями. Другими словами, не является ли гипотеза 5 недоказуемой?
- Требуется исправить, обобщить и скомпилировать имеющиеся фрагментарные наброски доказательств, придав теории насыщения достаточную формализованность.
Ссылки
- 1. http://circiter.github.io/saturation-theory-part-1
- 2. http://en.wikipedia.org/wiki/perfect_number
- 3. http://ru.wikipedia.org/wiki/совершенное_число
- 4. Никомах Геразский. Введение в арифметику / пер. Щетников А.И.
- 5. Nicomachus of Gerasa. Introduction to Arithmetic / пер. Martin Luther D’Ooge
- 6. Sylvester J.J. Sur les nombres dits de Hamilton. 1887
- 7. Pomerance’s Heuristic that Odd Perfect Numbers are Unlikely http://web.archive.org/web/20061229094011/http://oddperfect.org/pomerance.html
Приложение A
В данном приложении представлена «заплатка», предположительно исправляющая (обобщающая) доказательство наблюдения 1 (само доказательство находится в первой части этой серии сообщений).
Определение: Функция Эйлера 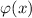 равна количеству чисел, меньших
равна количеству чисел, меньших  и взаимно
простых с ним.
и взаимно
простых с ним.
Предложение: Известно, что для степени  простого
простого 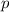 выполняется
выполняется

В наброске доказательства наблюдения 1 использовалась
конструктивная китайская теорема об остатках, дававшая решение (по модулю 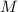 ) вида
) вида
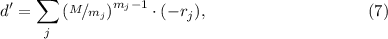
где
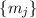 – все различные факторы числа
– все различные факторы числа 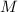 для случае его факторизации без повторов:
для случае его факторизации без повторов:
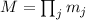 .
.
В общем случае, число 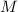 факторизуется в виде
факторизуется в виде 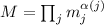 (каноническое
разложение), где
(каноническое
разложение), где 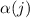 – максимальная степень простого делителя
– максимальная степень простого делителя 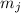 , на которую делится
, на которую делится
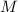 . В заключительной части предыдущего сообщения я предположил, что можно, при применении
К.Т.О., вместо простых чисел
. В заключительной части предыдущего сообщения я предположил, что можно, при применении
К.Т.О., вместо простых чисел 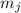 использовать взаимно простые модули
использовать взаимно простые модули 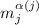 . Теперь
я уверен, что это действительно можно сделать.
. Теперь
я уверен, что это действительно можно сделать.
Обозначим 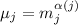 . Очевидно,
. Очевидно, 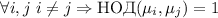 (т.е. модули
(т.е. модули 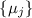 попарно взаимно просты). Тогда конструктивная версия К.Т.О.
даст решение в виде
попарно взаимно просты). Тогда конструктивная версия К.Т.О.
даст решение в виде

заменяющим решение
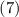 .
.
Из 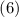 следует, что показатель степени в
следует, что показатель степени в 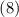 равен
равен 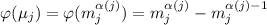 . Очевидно,
. Очевидно,
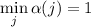 , а из-за нечётности
, а из-за нечётности 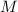 выполняется
выполняется 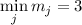 . Отсюда,
. Отсюда,
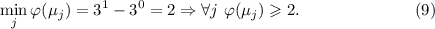
(Полная роль этого неравенства мне пока неясна, а далее пока будет достаточно условия  .)
.)
Здесь будут пропущены рассуждения, аналогичные рассуждениям из первого сообщения (выполненным
для 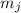 , а не для
, а не для 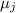 ), приводящие в настоящем случае к необходимости проверки делимости
выражения
), приводящие в настоящем случае к необходимости проверки делимости
выражения 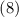 на модули
на модули 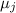 . Из этих рассуждений вытекает задача
проверки дробности выражения
. Из этих рассуждений вытекает задача
проверки дробности выражения
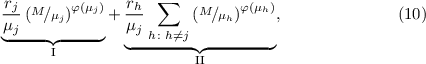
полученного из
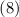 делением его на
делением его на 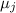 (для произвольного
(для произвольного 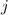 ) и выноса одного из
слагаемых суммы за её пределы.
) и выноса одного из
слагаемых суммы за её пределы.
Легко видеть, что подвыражение 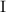 всегда больше нуля, а вот подвыражение
всегда больше нуля, а вот подвыражение  может быть равно нулю (если все факторы числа
может быть равно нулю (если все факторы числа 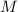 равны друг другу).
равны друг другу).
Дальнейшие рассуждения полностью аналогичны уже выполненным в первом сообщении. Я лишь кратко
повторю самое важное. Итак, в подвыражении  мы можем поделить
мы можем поделить 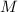 на
на 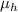 , что
даст целое число, большее единицы. Единица могла бы получиться только если в наличии имелся бы
ровно один модуль
, что
даст целое число, большее единицы. Единица могла бы получиться только если в наличии имелся бы
ровно один модуль 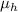 , но в таком случае всё подвыражение
, но в таком случае всё подвыражение  было бы нулём (см.
предыдущий абзац), а значит – целым числом. Если же дробь
было бы нулём (см.
предыдущий абзац), а значит – целым числом. Если же дробь 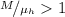 , то после
возведения в ненулевую степень — cf. неравенство
, то после
возведения в ненулевую степень — cf. неравенство 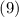 — получится целое
число, большее единицы и делящееся на
— получится целое
число, большее единицы и делящееся на 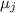 (т.к.
(т.к. 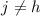 ). Это приводит к целочисленности
подвыражения
). Это приводит к целочисленности
подвыражения  .
.
В подвыражении 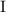 дробь
дробь 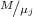 – целая. Но важно, что такая дробь
«вычеркивает»
– целая. Но важно, что такая дробь
«вычеркивает» 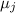 из
из 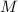 , и, поэтому, сама дробь на
, и, поэтому, сама дробь на 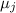 второй раз уже не делится.
Результат возведения в степень
второй раз уже не делится.
Результат возведения в степень 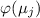 тоже не будет делиться на
тоже не будет делиться на 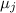 (составляющим
(составляющим
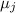 факторам неоткуда взяться). Число
факторам неоткуда взяться). Число 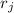 , по аналогии с предыдущим сообщением, определим
как остаток от деления частичной суммы
, по аналогии с предыдущим сообщением, определим
как остаток от деления частичной суммы 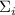 на модуль
на модуль 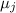 . Такой остаток меньше
. Такой остаток меньше
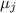 и делиться на
и делиться на 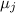 не может. В итоге получается, что подвыражение
не может. В итоге получается, что подвыражение 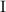 – есть
дробь со знаменателем
– есть
дробь со знаменателем 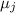 и числителем, не делящимся на
и числителем, не делящимся на 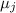 . Т.е. подвыражение
. Т.е. подвыражение
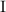 – дробное число. (Здесь стоит подчеркнуть ещё раз, что
– дробное число. (Здесь стоит подчеркнуть ещё раз, что 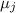 вычеркивается из
вычеркивается из 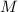 и, в результате,
и, в результате, 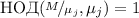 , поэтому дробность или
целочисленность
, поэтому дробность или
целочисленность 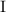 полностью определяется делимостью
полностью определяется делимостью 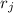 на
на 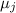 .)
.)
Всё это говорит о том, что выражение 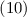 , как сумма дробного и
целого чисел, – есть число дробное. Другими словами, выражение
, как сумма дробного и
целого чисел, – есть число дробное. Другими словами, выражение 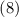 не
делится на
не
делится на 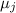 , а из произвольности
, а из произвольности 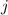 получается, что
получается, что 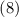 не
делится вообще ни на один из модулей
не
делится вообще ни на один из модулей 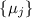 .
.
Можно ли считать, как думал я при написании предварительной версии этого сообщения, что, по
аналогии с доказательством из первого сообщения, некратность делителя каждому из 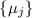 доказывает шаг индукции из-за противоречия с «критериями делителя» (см. первое сообщение;
кратко: делитель
доказывает шаг индукции из-за противоречия с «критериями делителя» (см. первое сообщение;
кратко: делитель 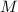 должен делиться хотя бы на один из
должен делиться хотя бы на один из 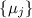 )? Нет! Если текущий делитель
)? Нет! Если текущий делитель
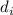 не делится на некоторый
не делится на некоторый 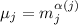 , то это не значит, что он не делится,
скажем для примера, на
, то это не значит, что он не делится,
скажем для примера, на 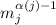 .
.
Фактически, рассуждения, приведённые выше в этой заплатке действуют только если 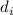 принадлежит подходящему подмножеству множества
принадлежит подходящему подмножеству множества 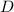 делителей числа
делителей числа 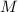 . Такое подмножество
должно состоять из делителей, могущих быть «собранными» из модулей
. Такое подмножество
должно состоять из делителей, могущих быть «собранными» из модулей 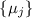 . Для других
делителей описанный аргумент не работает. Но это же и подсказывает возможный гипотетический путь
завершения доказательства шага индукции.
. Для других
делителей описанный аргумент не работает. Но это же и подсказывает возможный гипотетический путь
завершения доказательства шага индукции.
В первом сообщении мы имели дело с системой модулей 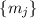 , в настоящем сообщении – с
, в настоящем сообщении – с
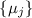 . Это – предельные, крайние случаи, и, возможно, разрешить возникшую проблему
удастся с помощью введения большего количества «промежуточных» систем модулей. Этот зыбкий
путь опирается на ряд вспомогательных [остающихся пока недоказанными] гипотез.
. Это – предельные, крайние случаи, и, возможно, разрешить возникшую проблему
удастся с помощью введения большего количества «промежуточных» систем модулей. Этот зыбкий
путь опирается на ряд вспомогательных [остающихся пока недоказанными] гипотез.
Определение
Пусть 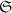 – семейство всех возможных систем модулей (для данного числа
– семейство всех возможных систем модулей (для данного числа  ). Для
). Для
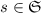 обозначим
обозначим 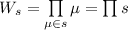 . Для нужд К.Т.О.
необходимо, чтобы выполнялось
. Для нужд К.Т.О.
необходимо, чтобы выполнялось 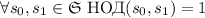 .
.
Каждая система  порождает подмножество
порождает подмножество  , такое, что каждый
делитель
, такое, что каждый
делитель  конструируется из этих модулей, т.е.
конструируется из этих модулей, т.е. 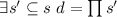 .
.
Гипотеза 6 (без доказательства): 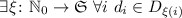 . Т.е. гипотетическая функция
. Т.е. гипотетическая функция
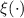 классифицирует делители по их индексам в последовательности
классифицирует делители по их индексам в последовательности 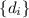 и
сопоставляет им подходящие системы модулей.
и
сопоставляет им подходящие системы модулей.
Идея доказательства: Может быть эту гипотезу и не надо доказывать. :) Может быть сгодится
аргумент «по определению». Будем просто перебирать всевозможные системы модулей из
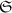 и для каждой
и для каждой 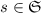 находить подходящее подмножество (максимальное по
включению)
находить подходящее подмножество (максимальное по
включению)  . Табулирование индексов входящих в
. Табулирование индексов входящих в 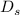 делителей и даст требуемое
отображение
делителей и даст требуемое
отображение 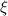 .
. 
Предложение 1: 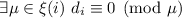 . Это просто обновлённый критерий делителя; само утверждения я нахожу достаточно
очевидным.
. Это просто обновлённый критерий делителя; само утверждения я нахожу достаточно
очевидным.
Гипотеза 7 (без доказательства)
Пусть 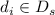 для некоторого
для некоторого 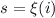 (см. гипотезу 6) и пусть система сравнений
(см. гипотезу 6) и пусть система сравнений  (где
(где 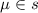 пробегает все возможные
значения) имеет решение
пробегает все возможные
значения) имеет решение 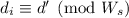 (N.B., по модулю
(N.B., по модулю 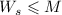 , а не
обязательно
, а не
обязательно 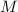 ), для некоторого числа
), для некоторого числа 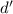 [даваемого К.Т.О.]. Тогда, если
[даваемого К.Т.О.]. Тогда, если 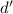 не делится на
некоторый
не делится на
некоторый 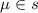 , то и
, то и 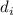 не делится на
не делится на 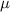 . Кратко:
. Кратко: 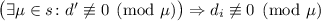 .
.
Соображения по доказательству: Я не знаю как доказать эту гипотезу, но все претензии здесь к
китайской теореме об остатках. :) Я просто принимаю за должное, что если оценка делителя, т.е.
решение 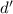 , полученное применением этой теоремы, делится на
, полученное применением этой теоремы, делится на 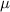 , то и настоящий делитель
, то и настоящий делитель
 должен делиться на
должен делиться на 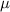 (разве не разумно ожидать, что оценка или приближение некоторого
объекта, должны обладать большинством свойств этого объекта?). Проблема здесь в том, что
основная теорема арифметики, в таком случае, приводит к равенству
(разве не разумно ожидать, что оценка или приближение некоторого
объекта, должны обладать большинством свойств этого объекта?). Проблема здесь в том, что
основная теорема арифметики, в таком случае, приводит к равенству  , но в реальности
численные значения делителя и его К.Т.О.-оценки вроде как не обязаны совпадать… Одна из
«дырок» теории насыщения, возможно, находится именно здесь.
, но в реальности
численные значения делителя и его К.Т.О.-оценки вроде как не обязаны совпадать… Одна из
«дырок» теории насыщения, возможно, находится именно здесь.
На основе этих дополнительных определений и гипотез можно продолжить говорить об основном доказательстве [наблюдения 1].
Итак, подразумевается, что для любой  действительна прямая адаптация
аргумента, приведённого в начале описания этой заплатки. Применение такого аргумента приводит к
выводу о том, что на некотором шаге индуктивного доказательства наблюдения 1, решение системы
действительна прямая адаптация
аргумента, приведённого в начале описания этой заплатки. Применение такого аргумента приводит к
выводу о том, что на некотором шаге индуктивного доказательства наблюдения 1, решение системы 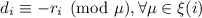 , а именно
число
, а именно
число 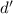 , оказывается некратным каждому из модулей
, оказывается некратным каждому из модулей 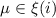 . Из гипотезы 7 тогда следует, что и
. Из гипотезы 7 тогда следует, что и 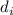 не делится ни на один из
не делится ни на один из
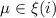 . Но это нарушает новый критерий делителя из предложения 1 и приводит к желаемому противоречию, доказывая, т.о., шаг индукции (от
противного) и теперь наконец-то завершает доказательство.
. Но это нарушает новый критерий делителя из предложения 1 и приводит к желаемому противоречию, доказывая, т.о., шаг индукции (от
противного) и теперь наконец-то завершает доказательство.
Ещё раз подчёркиваю, что приведённый в настоящем приложении фрагмент является именно «заплаткой», требующей своего наложения на исходное доказательство наблюдения 1 из первого сообщения. Как нибудь потом я обязательно напишу полное доказательство, но пока заплатка лучше чем ничего… :)